Lecture
We have had many cases to see how important the basic numerical characteristics of random variables are in probability theory: mathematical expectation and variance for one random variable, mathematical expectation and the correlation matrix for a system of random variables. The art of using numerical characteristics, leaving as far as possible the laws of distribution, is the basis of applied probability theory. The apparatus of numerical characteristics is a very flexible and powerful apparatus, which makes it relatively easy to solve many practical problems.
A completely similar apparatus is used in the theory of random functions. For random functions, the simplest basic characteristics similar to the numerical characteristics of random variables are also introduced, and the rules of actions with these characteristics are established. Such a device is sufficient to solve many practical problems.
In contrast to the numerical characteristics of random variables that provide certain numbers, the characteristics of random functions are, in general, not numbers, but functions.
Expectation of random function 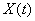 is defined as follows. Consider the cross section of a random function
is defined as follows. Consider the cross section of a random function 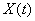 with fixed
with fixed 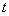 . In this section we have the usual random variable; we define its expectation. Obviously, in the general case it depends on
. In this section we have the usual random variable; we define its expectation. Obviously, in the general case it depends on 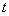 i.e. it represents some function
i.e. it represents some function 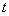 :
:
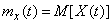 . (15.3.1)
. (15.3.1)
Thus, the mathematical expectation of a random function 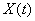 called non-random function
called non-random function 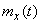 which for every argument value
which for every argument value 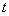 equal to the mathematical expectation of the corresponding cross section of a random function.
equal to the mathematical expectation of the corresponding cross section of a random function.
In terms of meaning, the expectation of a random function is some average function, around which the concrete implementations of the random function vary in various ways.
In fig. 15.3.1 thin lines show the implementation of a random function, a bold line is its expectation.
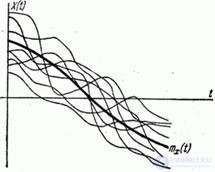
Fig. 15.3.1.
Similarly, the variance of a random function is determined.
Variance random function 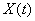 called non-random function
called non-random function 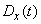 whose value for each
whose value for each 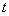 equal to the variance of the corresponding cross section of the random function:
equal to the variance of the corresponding cross section of the random function:
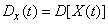 . (15.3.2)
. (15.3.2)
Variance of a random function at each 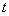 characterizes the scatter of possible implementations of a random function relative to the mean, in other words, the “degree of randomness” of a random function.
characterizes the scatter of possible implementations of a random function relative to the mean, in other words, the “degree of randomness” of a random function.
Obviously 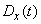 there is a non-negative function. Taking from it the square root, we obtain the function
there is a non-negative function. Taking from it the square root, we obtain the function 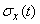 - standard deviation of the random function:
- standard deviation of the random function:
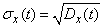 . (15.3.3)
. (15.3.3)
Expectation and variance are very important characteristics of a random function; however, these characteristics are not enough to describe the main features of the random function. To see this, consider two random functions. 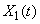 and
and 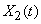 , visually depicted by the family of realizations in fig. 15.3.2 and 15.3.3.
, visually depicted by the family of realizations in fig. 15.3.2 and 15.3.3.

Fig. 15.3.2.
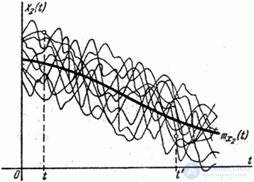
Fig. 15.3.3.
Do random functions 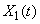 and
and 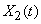 approximately the same expectation and variance; however, the nature of these random functions is dramatically different. For random function
approximately the same expectation and variance; however, the nature of these random functions is dramatically different. For random function 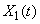 (fig. 15.3.2) is characterized by a smooth, gradual change. If, for example, at the point
(fig. 15.3.2) is characterized by a smooth, gradual change. If, for example, at the point 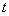 random function
random function 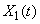 took a value significantly higher than the average, it is very likely that at the point
took a value significantly higher than the average, it is very likely that at the point 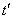 it will also take a value greater than average. For random function
it will also take a value greater than average. For random function 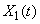 characterized by a pronounced dependence between its values at different
characterized by a pronounced dependence between its values at different 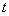 . In contrast, a random function
. In contrast, a random function 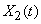 (fig. 15.3.3) has a sharply oscillating character with irregular, erratic fluctuations. Such a random function is characterized by a rapid decay of the dependence between its values with increasing distance along
(fig. 15.3.3) has a sharply oscillating character with irregular, erratic fluctuations. Such a random function is characterized by a rapid decay of the dependence between its values with increasing distance along 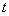 between them.
between them.
Obviously, the internal structure of both random processes is completely different, but this difference is not captured by either expectation or dispersion; for its description it is necessary to maintain a special characteristic. This characteristic is called the correlation function (otherwise, the autocorrelation function). The correlation function characterizes the degree of dependence between the cross sections of a random function relating to different 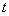 .
.
Let there be a random function 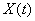 (fig. 15.3.4); Consider two of its sections relating to different points:
(fig. 15.3.4); Consider two of its sections relating to different points: 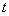 and
and 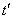 i.e. two random variables
i.e. two random variables 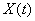 and
and 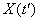 . Obviously, with close values
. Obviously, with close values 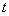 and
and 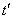 magnitudes
magnitudes 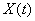 and
and 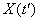 are closely related: if the value
are closely related: if the value 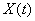 took some value, then the value
took some value, then the value 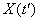 is likely to take a value close to it. It is also obvious that with an increase in the interval between sections
is likely to take a value close to it. It is also obvious that with an increase in the interval between sections 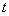 ,
, 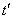 magnitude dependence
magnitude dependence 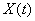 and
and 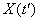 should generally decrease.
should generally decrease.
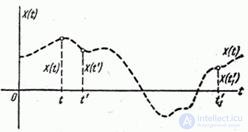
Fig. 15.3.4.
Degree of dependence 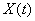 and
and 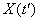 can be largely characterized by their correlation point; obviously, it is a function of two arguments
can be largely characterized by their correlation point; obviously, it is a function of two arguments 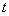 and
and 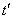 . This function is called the correlation function.
. This function is called the correlation function.
Thus, the correlation function of the random function 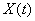 called the non-random function of two arguments
called the non-random function of two arguments 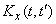 which with every pair of values
which with every pair of values 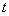 ,
, 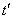 equal to the correlation moment of the corresponding sections of the random function:
equal to the correlation moment of the corresponding sections of the random function:
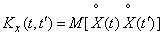 , (15.3.4)
, (15.3.4)
Where
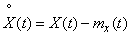 ,
, 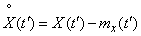 .
.
Let's return to examples of random functions.  and
and 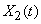 (fig. 15.3.2 and 15.3.3). We see now that with the same expectation and variance, random functions
(fig. 15.3.2 and 15.3.3). We see now that with the same expectation and variance, random functions 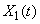 and
and 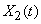 have completely different correlation functions. Correlation function of a random function
have completely different correlation functions. Correlation function of a random function 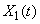 decreases slowly as the gap increases
decreases slowly as the gap increases 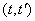 ; on the contrary, the correlation function of a random function
; on the contrary, the correlation function of a random function 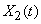 decreases rapidly with increasing this gap.
decreases rapidly with increasing this gap.
Find out what the correlation function turns to. 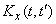 when her arguments match. Putting
when her arguments match. Putting 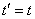 , we have:
, we have:
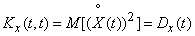 , (15.3.5)
, (15.3.5)
i.e.  the correlation function is drawn to the variance of the random function.
the correlation function is drawn to the variance of the random function.
Thus, the need for dispersion as a separate characteristic of a random function disappears: as the main characteristics of a random function, it suffices to consider its expectation and correlation function.
Since the correlation moment of two random variables  and
and  does not depend on the sequence in which these quantities are considered, the correlation function is symmetric with respect to its arguments, i.e. it does not change when the arguments change places:
does not depend on the sequence in which these quantities are considered, the correlation function is symmetric with respect to its arguments, i.e. it does not change when the arguments change places:
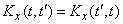 . (15.3.6)
. (15.3.6)
If to draw the correlation function 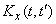 in the form of a surface, then this surface will be symmetric about the vertical plane
in the form of a surface, then this surface will be symmetric about the vertical plane 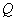 passing through the bisector of the angle
passing through the bisector of the angle 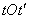 (fig. 15.3.5).
(fig. 15.3.5).
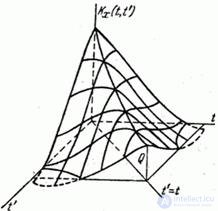
Fig. 15.3.5.
We note that the properties of the correlation function naturally follow from the properties of the correlation matrix of a system of random variables. Indeed, we replace the approximately random function. 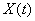 system
system 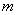 random variables
random variables 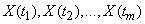 . By increasing
. By increasing 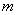 and, accordingly, the reduction of the intervals between the arguments of the correlation matrix of the system, which is a table of two inputs, in the limit goes into the function of two continuously changing arguments, which has similar properties. The symmetry property of the correlation matrix with respect to the main diagonal is transferred to the symmetry property of the correlation function (15.3.6). On the main diagonal of the correlation matrix are the variances of random variables; similarly with
and, accordingly, the reduction of the intervals between the arguments of the correlation matrix of the system, which is a table of two inputs, in the limit goes into the function of two continuously changing arguments, which has similar properties. The symmetry property of the correlation matrix with respect to the main diagonal is transferred to the symmetry property of the correlation function (15.3.6). On the main diagonal of the correlation matrix are the variances of random variables; similarly with 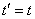 correlation function
correlation function 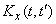 turns into a dispersion
turns into a dispersion 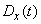 .
.
In practice, if you want to build a correlation function of a random function 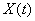 , usually come in the following way: set by a number of equally spaced argument values and build the correlation matrix of the resulting system of random variables. This matrix is nothing but a table of values of the correlation function for a rectangular grid of argument values on the plane.
, usually come in the following way: set by a number of equally spaced argument values and build the correlation matrix of the resulting system of random variables. This matrix is nothing but a table of values of the correlation function for a rectangular grid of argument values on the plane. 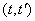 . Further, by interpolating or approximating, we can construct a function of two arguments
. Further, by interpolating or approximating, we can construct a function of two arguments 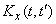 .
.
Instead of the correlation function 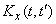 You can use the normalized correlation function:
You can use the normalized correlation function:
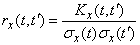 , (15.3.7)
, (15.3.7)
which is the correlation coefficient of the quantities 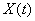 ,
, 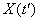 . The normalized correlation function is similar to the normalized correlation matrix of a system of random variables. With
. The normalized correlation function is similar to the normalized correlation matrix of a system of random variables. With 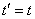 normalized correlation function is equal to one:
normalized correlation function is equal to one:
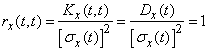 . (15.3.8)
. (15.3.8)
Let us find out how the basic characteristics of a random function change during elementary operations on it: when adding a nonrandom term and when multiplying by a nonrandom factor. These non-random terms and factors can be both constant values and, in general, functions.  .
.
Let's add to the random function  nonrandom term
nonrandom term  . Get a new random function:
. Get a new random function:
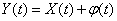 . (15.3.9)
. (15.3.9)
By the theorem of addition of mathematical expectations:
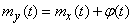 , (15.3.10)
, (15.3.10)
that is, when a nonrandom term is added to a random function, the same nonrandom term is added to its expectation.
Define the correlation function of a random function 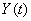 :
:
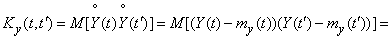
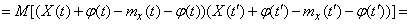
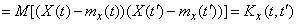 , (15.3.11)
, (15.3.11)
that is, by adding a nonrandom term, the correlation function of a random function does not change.
Multiply random function 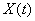 to a non-random factor
to a non-random factor 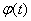 :
:
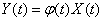 . (15.3.12)
. (15.3.12)
Carrying a non-random value 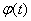 as a sign of mathematical expectation, we have:
as a sign of mathematical expectation, we have:
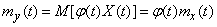 , (15.3.13)
, (15.3.13)
that is, when a random function is multiplied by a nonrandom factor, its expectation is multiplied by the same factor.
Determine the correlation function:
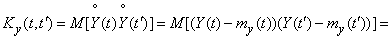
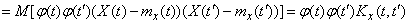 , (15.3.14)
, (15.3.14)
that is, when multiplying a random function by a nonrandom function 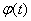 its correlation function is multiplied by
its correlation function is multiplied by 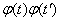 .
.
In particular, when 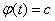 (not dependent on
(not dependent on 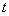 ), the correlation function is multiplied by
), the correlation function is multiplied by 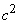 .
.
Using the derived properties of the characteristics of random functions, in some cases it is possible to significantly simplify operations with them. In particular, when it is necessary to investigate the correlation function or the variance of a random function, you can advance from it to the so-called centered function:
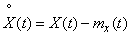 . (3/15/15)
. (3/15/15)
The expectation of a centered function is identically zero, and its correlation function coincides with the correlation function of a random function 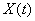 :
:
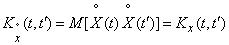 . (3/15/16)
. (3/15/16)
In the study of issues related to the correlation properties of random functions, in the future we will always move from random functions to the corresponding centered functions, marking this with 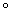 at the top of the function sign.
at the top of the function sign.
Sometimes, besides centering, rationing of random functions is also applied. Normalized is called a random function of the form:
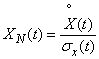 . (15.3.17)
. (15.3.17)
Correlation function of the normalized random function 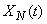 equals
equals
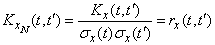 , (15.3.18)
, (15.3.18)
and its variance is one.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis