Expected value

The mathematical expectation is the average value of a random variable (this is the probability distribution of a random variable, considered in probability theory) ^[1] . In English literature it is denoted by 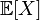^[2] (for example, from the English. Expected value or German Erwartungswert ), in Russian - 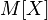(perhaps from the English. Mean value or German. Mittelwert , and possibly from the "Mathematical expectation"). The statistics often use the designation .

Definition [edit]

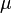Let probabilistic space be given 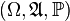and a random variable defined on it 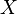. That is, by definition, 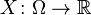- measurable function. If there is a Lebesgue integral from 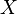in space 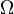, it is called the expectation, or average (expected) value, and is denoted by 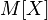or .

Basic formulas for expectation [edit]

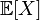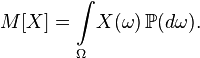
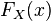• If a - the distribution function of a random variable, then its expectation is given by the Lebesgue – Stieltjes integral:

.

Mathematical expectation of a discrete distribution [edit]

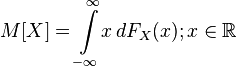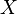• If a - discrete random variable with distribution

,

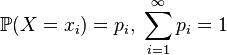then it follows directly from the definition of the Lebesgue integral that

.

Mathematical expectation of an integer value [edit]

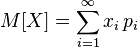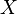• If a - positive integer random variable (special case discrete), having a probability distribution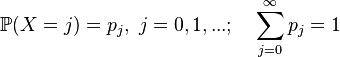

then its expectation can be expressed in terms of the generating function of the sequence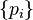

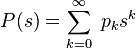
as the value of the first derivative in the unit: 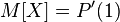. If the expectation 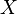endlessly then 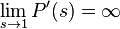and we will write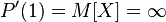

Now take the generating function 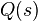sequences of tails of distribution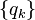

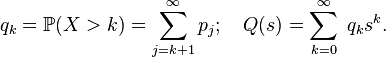
This generating function is associated with a previously defined function. 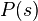property: 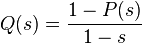at 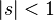. From this, by the mean-theorem, it follows that the expectation is equal to just the value of this function in the unit:

Mathematical expectation of absolutely continuous distribution [edit]

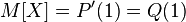
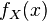• The expectation of an absolutely continuous random variable whose distribution is given by the density equal to

.

Mathematical expectation of a random vector [edit]

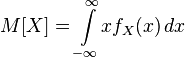Let be 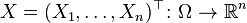- random vector. Then by definition

,

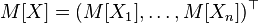that is, the expectation of a vector is determined componentwise.

Mathematical expectation of the conversion of a random variable [edit]

Let be 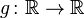- Borel function, such that a random variable 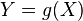has a finite mathematical expectation. Then the formula is valid for him:

,

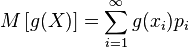if a 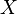has a discrete distribution;

,

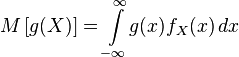if a 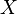has an absolutely continuous distribution.

If the distribution 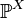random variable 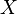general view then

.

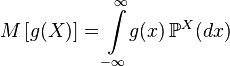In the special case when 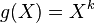, Expected value 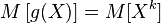called 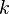th moment of a random variable.

The simplest properties of the expectation [edit]

• The mathematical expectation of a number is the number itself.

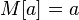
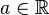- constant;

• The expectation is linear, that is

,

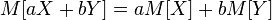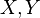Where - random variables with finite mathematical expectation, and 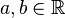- arbitrary constants;

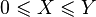• Expectation preserves inequalities, that is, if almost sure and 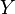- a random variable with a finite mathematical expectation, then a mathematical expectation of a random variable 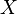also of course

;

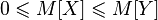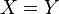• The expectation does not depend on the behavior of the random variable at the probability zero event, that is, if almost surely

.

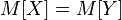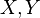• Mathematical expectation of the product of two independent random variables equal to the product of their mathematical expectations

.

Additional properties of expectation [edit]

• Markov's inequality;
• Levi's theorem on monotone convergence;
• Lebesgue's theorem on majorized convergence;
• Wald's identity;
• Lemma Fatou.
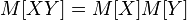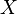• Mathematical expectation of a random variable can be expressed through its moments generating function 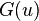as the value of the first derivative at zero: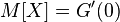

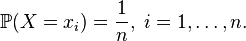Examples [edit]

• Let the random variable have a discrete uniform distribution, that is, Then her expectation is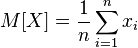

equal to the arithmetic average of all received values.

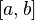• Let the random variable has a continuous uniform distribution on the interval where 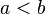. Then its density is 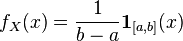and the expectation is

.

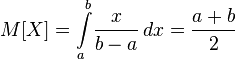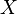• Let the random variable has a standard Cauchy distribution. Then

,

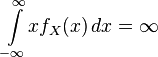i.e. expectation 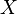undefined.

Notes [edit]

See also [edit]