Uniform distribution of random variable.

Lecture



The continuous random variable X is evenly distributed in the interval [ a; c ] if its probability density in this interval is constant, i.e. if all values ​​in this interval are equally likely:

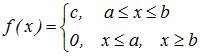Uniform distribution of random variable. (8.1)

The value of the constant с is determined from the normalization condition:

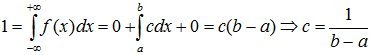Uniform distribution of random variable. . (8.2)

Distribution function:

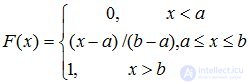Uniform distribution of random variable. , (8.3)

The numerical characteristics of a uniformly distributed random variable are defined as:

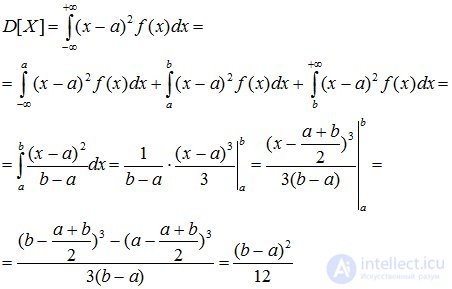Uniform distribution of random variable. (8.4)

Uniform distribution of random variable. (8.5)

The standard deviation of the uniform distribution is

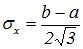Uniform distribution of random variable. (8.6)

The uniform distribution of a random variable is completely determined by two parameters: a and b , the interval at which the random variable is defined.

If necessary, you can determine the parameters a and b of the uniform distribution of the known values ​​of the expectation m X   and variance D x random variable. For this, a system of equations is made up of the following form:

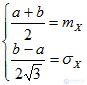Uniform distribution of random variable. , (8.7)

from which the desired parameters are determined.

The probability of a uniformly distributed random variable falling into the interval [α, β) is determined as follows:

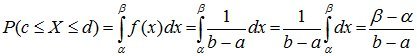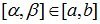
Uniform distribution of random variable. where Uniform distribution of random variable.

 

Continuous uniform distribution
Probability density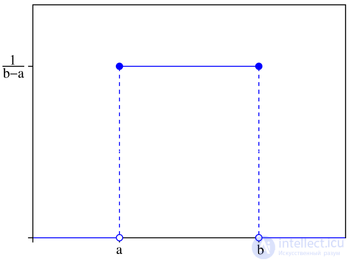
Uniform distribution of random variable.
Distribution function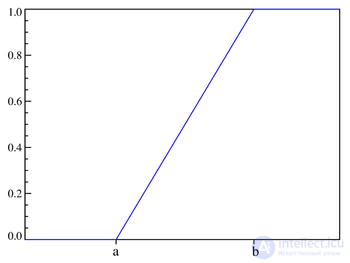
Uniform distribution of random variable.
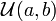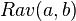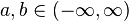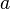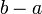Designation Uniform distribution of random variable. , Uniform distribution of random variable.
Options Uniform distribution of random variable. , Uniform distribution of random variable. —Shift factor Uniform distribution of random variable. - scale factor
Carrier 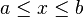Uniform distribution of random variable.
Probability density 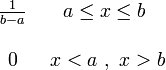Uniform distribution of random variable. b \ end {matrix}">
Distribution function 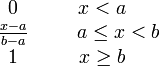Uniform distribution of random variable.
Expected value 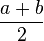Uniform distribution of random variable.
Median 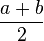Uniform distribution of random variable.
Fashion any number of segment 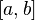Uniform distribution of random variable.
Dispersion 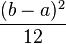Uniform distribution of random variable.
Asymmetry coefficient 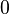Uniform distribution of random variable.
Coefficient of kurtosis 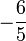Uniform distribution of random variable.
Informational entropy 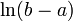Uniform distribution of random variable.
Generating function of moments 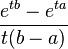Uniform distribution of random variable.
Characteristic function 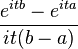Uniform distribution of random variable.

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Probability theory. Mathematical Statistics and Stochastic Analysis

Terms: Probability theory. Mathematical Statistics and Stochastic Analysis