2.3. Frequency, or statistical probability, of an event

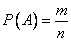, (2.2.1)

The formula (2.2.1) for the direct calculation of probabilities is applicable only when the experience, as a result of which an event of interest to us may appear, has a symmetry of possible outcomes (reduced to a diagram of cases). It is obvious that not every experience can be reduced to the scheme of cases, and there is an extensive class of events, the probabilities of which cannot be calculated by the formula (2.2.1). Consider, for example, an improperly made, asymmetrical dice. The loss of a certain face will no longer be characterized by a probability of 1/6; at the same time, it is clear that for this particular asymmetrical bone, the loss of this face has a certain probability, indicating how often this edge should appear on average during repeated throwing. It is obvious that the probabilities of such events as “hitting the target when fired”, “failure of radio tubes within one hour of work” or “penetration of armor by a fragment of a projectile” also cannot be calculated using the formula (2.2.1), since relevant experiments to the scheme of cases are not reduced. At the same time, it is clear that each of the listed events has a certain degree of objective possibility, which in principle can be measured numerically and which, if such experiments are repeated, will be reflected in the relative frequency of the corresponding events. Therefore, we will assume that each event associated with a mass of homogeneous experiments — reduced to a pattern of cases or not — has a certain probability that is between zero and one. For events that are reduced to the scheme of cases, this probability can be calculated directly by the formula (2.2.1). For events that are not reducible to the pattern of cases, other methods of determining probabilities are used. All these methods are rooted in their experience, in experiment, and in order to get an idea of ​​these methods, it is necessary to understand the concept of the frequency of the event and the specificity of the organic connection that exists between probability and frequency.

If produced a series of 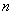experiences, in each of which some event could appear or not 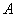then the frequency of the event 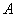in this series of experiments is called the ratio of the number of experiments in which the event appeared 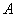to the total number of experiments performed.

The frequency of an event is often called its statistical probability (in contrast to the previously introduced "mathematical" probability).

We agree to designate the frequency (statistical probability) of an event. 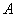familiar 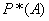. The frequency of the event is calculated based on the results of the experiment according to the formula

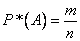, (2.3.1)

Where 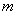- the number of occurrences 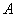; 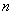- The total number of experiments performed.

With a small number of experiments, the frequency of the event is largely random and can vary significantly from one group of experiments to another. For example, with some ten throwing of a coin, it is possible that the emblem will appear only twice (the frequency of the emblem will be 0.2) with the other ten throws, we can easily get 8 coats of arms (frequency 0.8). However, with an increase in the number of experiments, the frequency increasingly loses its random character; random circumstances inherent in each individual experience, in the mass are mutually canceled, and the frequency tends to stabilize, approaching with a slight fluctuation to a certain average, constant value. For example, if you repeatedly throw a coin, the frequency of the appearance of the coat of arms will only slightly deviate from ½.

This property of “frequency stability”, repeatedly verified experimentally and confirmed by all the practical experience of humankind, is one of the most characteristic patterns observed in random phenomena. The mathematical formulation of this pattern was first given by J. Bernoulli in his theorem, which is the simplest form of the law of large numbers. J. Bernoulli proved that with an unlimited increase in the number of homogeneous independent experiments it can be argued with practical certainty that the frequency of an event will differ as little as desired from its probability in a separate experiment.

The connection between the frequency of an event and its probability is a deep, organic connection. These two concepts are essentially inseparable. Indeed, when we assess the degree of possibility of an event, we inevitably associate this assessment with a greater or lesser frequency of occurrence of similar events in practice. Describing the probability of an event by a certain number, we can not give this number a different real value and a different practical meaning than the relative frequency of occurrence of this event with a large number of experiments. Numerical evaluation of the degree of possibility of an event by means of probability has a practical meaning precisely because more probable events occur on average more often than less probable ones. And if practice definitely indicates that with an increase in the number of experiments, the frequency of an event tends to even out, approaching through a series of random deviations to a certain constant number, it is natural to assume that this number is the probability of an event.

We can check this assumption, naturally, only for such events, the probabilities of which can be directly calculated, i.e. for events that are reduced to the scheme of cases, since only for these events there is an exact way to calculate the mathematical probability. Numerous experiments carried out since the emergence of probability theory really support this assumption. They show that for an event that reduces to a pattern of cases, the frequency of an event with an increase in the number of experiments always approaches its probability. It is quite natural to assume that for an event that is not reducible to the pattern of cases, the same law remains in force and that the constant value to which the frequency of the event approaches as the number of experiments increases is nothing more than the probability of the event. Then the frequency of the event with a sufficiently large number of experiments can be taken as an approximate value of probability. They do this in practice, determining from the experience the probabilities of events that are not reducible to the pattern of cases.

It should be noted that the nature of the approach of frequency to probability with an increase in the number of experiments is somewhat different from the “striving for the limit” in the mathematical sense of the word.

When in mathematics we say that the variable 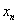with increasing 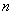aim for a constant limit 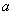then it means that the difference 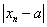becomes less than any positive number 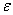for all values 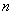starting with some fairly large number.

With regard to the frequency of the event and its probability, such a categorical statement cannot be made. Indeed, it is not physically impossible that, with a large number of experiments, the frequency of an event will significantly shy away from its probability; but such a significant evasion is highly unlikely, the less likely the greater the number of experiments. For example, when a coin is thrown 10 times it is physically possible (although unlikely) that the coat of arms will appear all 10 times and the frequency of the coat of arms will be 1; at 1000 throws, such an event is still physically possible, but it acquires such a small probability that it can be safely considered practically impracticable. Thus, with an increase in the number of experiments, the frequency approaches the probability, but not with full confidence, but with a high probability, which, with a sufficiently large number of experiments, can be considered as practical accuracy.

In the theory of probability it is extremely common to have such a character of approximation of one value to another, and a special term has been introduced to describe it: “convergence in probability”.

It is said that 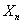converges in probability to value 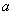if at any small 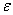probability of inequality 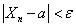with increasing 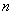unlimited approaches one.

Applying this term, we can say that with an increase in the number of experiments, the frequency of an event does not “tend” to the probability of an event, but “converges to it in probability”.

This property of frequency and probability set forth here so far without sufficient mathematical grounds, simply on the basis of practice and common sense, is the content of the Bernoulli theorem, which will be proved by us later (see Chapter 13).

Thus, by introducing the concept of the frequency of an event and using the connection between frequency and probability, we are able to attribute certain probabilities concluded between zero and one, not only events that are reduced to the pattern of cases, but also to those events that are not reduced to this pattern; in the latter case, the probability of an event can be approximately determined by the frequency of the event with a large number of experiments.

In the future, we will see that to determine the probability of an event that is not reduced to a pattern of cases, it is not always necessary to directly determine its frequency from experience. Probability theory has many ways to determine the probabilities of events indirectly, through the probabilities of other events associated with them. In essence, such indirect methods constitute the main content of the theory of probability. However, even with such indirect research methods, ultimately, one still has to refer to experimental data. The reliability and objective value of all practical calculations performed using the probability theory apparatus is determined by the quality and quantity of experimental data on which this calculation is performed.

In addition, in the practical application of probabilistic research methods, it is always necessary to be aware of whether the random phenomenon under investigation belongs to the category of mass phenomena, for which, at least for a certain period of time, the frequency stability property holds. Only in this case it makes sense to talk about probabilistic events, having in mind not the mathematical fiction, but the real characteristics of random phenomena.

For example, the expression “the probability of hitting an aircraft in an air battle for these conditions is 0.7” has a specific meaning, because air battles are thought of as mass operations that will be repeated several times under approximately similar conditions.

On the contrary, the expression “the probability that a given scientific problem is solved correctly is 0.7” does not have a specific meaning, and it would be methodologically incorrect to evaluate the likelihood of scientific propositions using methods of probability theory.