Lecture
Confidence interval is a term used in mathematical statistics with an interval (as opposed to a point) estimate of statistical parameters, which is preferable for a small sample size. A confidence interval is an interval that covers an unknown parameter with a given reliability.
The method of confidence intervals was developed by the American statistician Jerzy Neumann, based on the ideas of the English statistics by Ronald Fisher [ref 1] .
The confidence interval of the parameter 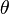 random distribution
random distribution 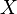 with a confidence level of 100% - p [note 1] , generated by the sample
with a confidence level of 100% - p [note 1] , generated by the sample 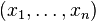 called interval with borders
called interval with borders 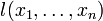 and
and 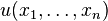 which are realizations of random variables
which are realizations of random variables 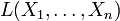 and
and 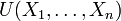 such that
such that
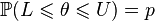 .
. Boundary points of the confidence interval 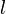 and
and 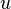 are called confidential limits .
are called confidential limits .
Interpretation of the confidence interval based on intuition will be as follows: if p is large (say, 0.95 or 0.99), then the confidence interval will almost certainly contain the true value 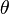 . [link 2]
. [link 2]
Another interpretation of the concept of a confidence interval: it can be considered as an interval of parameter values 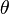 compatible with the experimental data and do not contradict them.
compatible with the experimental data and do not contradict them.
In Bayesian statistics, there is a similar, but different in some key details, definition of a confidence interval. Here is the estimated parameter 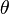 Itself is considered a random variable with a certain a priori distribution (in the simplest case - uniform), and the sample
Itself is considered a random variable with a certain a priori distribution (in the simplest case - uniform), and the sample 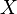 fixed (in classical statistics, exactly the opposite). Bayesian
fixed (in classical statistics, exactly the opposite). Bayesian 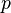 - confidence interval is an interval
- confidence interval is an interval 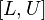 covering a parameter value
covering a parameter value 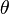 saposterory probability
saposterory probability 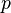 :
:
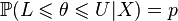 .
. As a rule, classical and Bayesian confidence intervals differ. In English literature, the Bayesian confidence interval is commonly referred to as the term credible interval , and the classic is called the confidence interval .
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis