Lecture
Before setting out the theorem of multiplication of probabilities, we introduce another important concept: the concept of independent and dependent events.
Event  called independent of the event
called independent of the event  if the probability of an event
if the probability of an event  does not depend on what happened
does not depend on what happened  or not.
or not.
Event  called event dependent
called event dependent  if the probability of event A changes depending on whether the event has occurred
if the probability of event A changes depending on whether the event has occurred  or not.
or not.
Consider examples.
1) The experience consists in throwing two coins; deals with events:
 - the appearance of the emblem on the first coin,
- the appearance of the emblem on the first coin,
 - The appearance of the emblem on the second coin.
- The appearance of the emblem on the second coin.
In this case, the probability of an event  does not depend on what happened
does not depend on what happened  or not; event
or not; event  whatever event
whatever event  .
.
2) In the urn two white balls and one black; two faces are removed from the urn one bowl at a time; deals with events:
 - the appearance of a white ball in the 1st person,
- the appearance of a white ball in the 1st person,
 - the appearance of a white ball in the 2nd person.
- the appearance of a white ball in the 2nd person.
Event probability  before something is known about the event
before something is known about the event  equal to 2/3. If it became known that the event
equal to 2/3. If it became known that the event  happened, then the probability of an event
happened, then the probability of an event  becomes equal to ½, from which we conclude that the event
becomes equal to ½, from which we conclude that the event  depends on the event
depends on the event  .
.
Event probability  calculated on condition that another event has occurred
calculated on condition that another event has occurred  is called the conditional probability of an event
is called the conditional probability of an event  and is denoted by
and is denoted by
 .
.
For the conditions of the last example
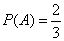 ;
; 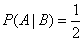 .
.
Condition independence event  from the event
from the event  can be written as:
can be written as:
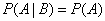 ,
,
and the condition of dependence is in the form:
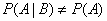 .
.
We proceed to the formulation and proof of the probability multiplication theorem.
The probability multiplication theorem is formulated as follows.
The probability of the product of two events is equal to the product of the probabilities of one of them by the conditional probability of the other, calculated under the condition that the first took place:
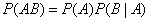 . (3.3.1)
. (3.3.1)
Let us prove the multiplication theorem for the scheme of cases. Let possible outcomes of experience be reduced to  For the sake of clarity, we will again depict them in the form
For the sake of clarity, we will again depict them in the form  points:
points:
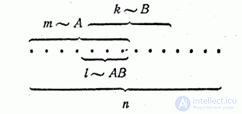
Suppose event  favorable
favorable  events
events  favorable
favorable  cases. Since we did not anticipate events
cases. Since we did not anticipate events  and
and  incompatible, then generally there are cases favorable and eventful
incompatible, then generally there are cases favorable and eventful  and event
and event  at the same time. Let the number of such cases
at the same time. Let the number of such cases 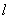 . Then
. Then
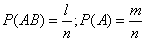 .
.
Calculate  i.e. conditional probability of an event
i.e. conditional probability of an event  under the assumption that
under the assumption that  took place. If it is known that the event
took place. If it is known that the event  happened then from the previously possible
happened then from the previously possible  cases remain possible only those
cases remain possible only those 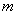 that favored the event
that favored the event  . Of them
. Of them 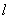 cases are favorable event
cases are favorable event  . Consequently,
. Consequently,
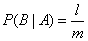 .
.
Substituting expressions 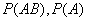 and
and  in formula (3.3.1), we obtain the identity. The theorem is proved.
in formula (3.3.1), we obtain the identity. The theorem is proved.
Obviously, when applying the multiplication theorem, it makes no difference which of the events  and
and  be considered the first, and which is the second, and the multiplication theorem can be written in this form:
be considered the first, and which is the second, and the multiplication theorem can be written in this form:
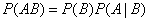 .
.
We point out the corollaries arising from the multiplication theorem.
Corollary 1. If an event  independent of event
independent of event  , then the event
, then the event  independent of event
independent of event  .
.
Evidence. Given that event  does not depend on
does not depend on  i.e.
i.e.
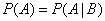 . (3.3.2)
. (3.3.2)
It is required to prove that the event  does not depend on
does not depend on  i.e.
i.e.
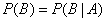 .
.
In the proof, we will assume that 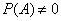 .
.
We write the probability theorem in two forms:
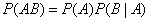 ,
,
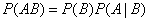 ,
,
from where
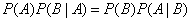
or, according to condition (3.3.2),
 . (3.3.3)
. (3.3.3)
We divide both sides of equality (3.3.3) into 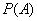 . We get:
. We get:
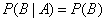 ,
,
Q.E.D.
Corollary 1 implies that the dependence or independence of events is always reciprocal. In this regard, it is fashionable to give the following new definition of independent events.
Two events are called independent if the appearance of one of them does not change the probability of the appearance of the other.
The notion of independence of events can be extended to the case of an arbitrary number of events. Several events are called independent if any of them does not depend on any aggregate of the others.
Corollary 2. The probability of the product of two independent events is equal to the product of the probabilities of these events.
The corollary follows directly from the definition of independent events.
The probability multiplication theorem can be generalized to the case of an arbitrary number of events. In general terms, it is formulated as follows.
The probability of producing several events is equal to the product of the probabilities of these events, and the probability of each subsequent event in order is calculated under the condition that all previous events occurred:
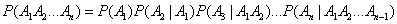 . (3.3.4)
. (3.3.4)
The proof can be given by the same method of complete induction.
In the case of independent events, the theorem is simplified and takes the form:
 , (3.3.5)
, (3.3.5)
those. the probability of the product of independent events is equal to the product of the probabilities of these events.
Applying the sign of the product, the theorem can be written in the form:
 . (3.3.6)
. (3.3.6)
Consider examples on the application of the probability multiplication theorem.
Example 1. In the urn 2 white and 3 black balls. Two balls are taken out of the urn in a row. Find the probability that both balls are white.
Decision. Denote:
 - the appearance of two white balls.
- the appearance of two white balls.
Event  is a product of two events:
is a product of two events:
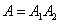 ,
,
Where 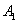 - the appearance of a white ball when first taken out,
- the appearance of a white ball when first taken out, 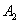 - the appearance of a white ball during the second removal.
- the appearance of a white ball during the second removal.
By the probability multiplication theorem
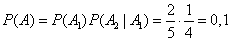 .
.
Example 2. The same conditions, but after first removing the ball returns to the urn, and the balls in the urn are mixed.
Decision. In this case, the event 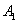 and
and 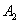 independent and
independent and
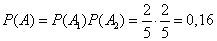 .
.
Example 3. Instrument operating over time.  , consists of three nodes, each of which, independently of the others, can over time
, consists of three nodes, each of which, independently of the others, can over time  refuse (fail). Failure of at least one node leads to failure of the device as a whole. During
refuse (fail). Failure of at least one node leads to failure of the device as a whole. During  reliability (probability of failure-free operation) of the first node is equal to
reliability (probability of failure-free operation) of the first node is equal to 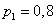 ; second
; second 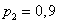 ; the third
; the third  . Find the reliability of the device as a whole.
. Find the reliability of the device as a whole.
Decision. Denoting:
 - trouble-free operation of devices,
- trouble-free operation of devices,
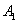 - trouble-free operation of the first node,
- trouble-free operation of the first node,
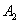 - trouble-free operation of the second node,
- trouble-free operation of the second node,
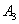 - trouble-free operation of the third node,
- trouble-free operation of the third node,
we have:
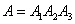 ,
,
whence by multiplication theorem for independent events
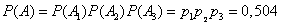 .
.
In practice, tasks are relatively rare in which you need to apply only the addition theorem or only the probability multiplication theorem. Usually both theorems have to be applied together. In this case, as a rule, the event whose probability is required to be determined is represented as the sum of several incompatible events (variants of this event), each of which in turn is a product of events.
Example 4. Three shots are fired at the same target. The probability of hitting the first, second and third shots are equal, respectively
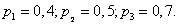
Find the probability that as a result of these three shots in the target will be exactly one hole.
Decision. Consider an event  - exactly one hit in the target. This event can be realized in several ways, i.e. splits into several incompatible variants: there may be a hit on the first shot, a miss on the second and third; or hit on the second shot, misses on the first and third; or, at last, misses at the first and second shots and hit at the third. Consequently,
- exactly one hit in the target. This event can be realized in several ways, i.e. splits into several incompatible variants: there may be a hit on the first shot, a miss on the second and third; or hit on the second shot, misses on the first and third; or, at last, misses at the first and second shots and hit at the third. Consequently,
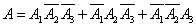 ,
,
Where 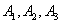 - hit on the first, second, third shots,
- hit on the first, second, third shots, 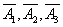 - a miss at the first, second, third shots.
- a miss at the first, second, third shots.
Applying the theorems of addition and multiplication of probabilities and using the property of opposite events, we find:
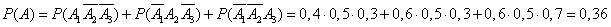 .
.
Example 5. In the conditions of the previous example, find the probability that there will be at least one hole in the target.
Decision. Consider an event  - at least one hit in the target. Using the same technique that was used in the previous example, the same notation, you can present the event
- at least one hit in the target. Using the same technique that was used in the previous example, the same notation, you can present the event  as a sum of incompatible options:
as a sum of incompatible options:
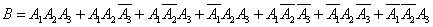 ,
,
find the probability of each variant by the multiplication theorem and add all these probabilities. However, this way of solving the problem is too complicated; here it is advisable from a direct event  go to the opposite:
go to the opposite:
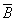 - not a single hit in the target.
- not a single hit in the target.
Obviously
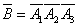 .
.
By the multiplication theorem
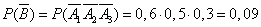 ,
,
from where
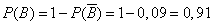 .
.
The last example illustrates the principle of the expediency of using opposite events in probability theory. It can be formulated as follows.
If the opposite event falls into a smaller number of variants than a direct event, then it makes sense, when calculating the probabilities, to switch to the opposite event.
Example 6. There is a battle ("duel") between two participants (aircraft, tanks, ships)  and
and  . By the side
. By the side  there are two shots left, on the side
there are two shots left, on the side  - one. Starts shooting
- one. Starts shooting  : he does by
: he does by  one shot and hits it with a probability of 0.2. If a
one shot and hits it with a probability of 0.2. If a  not struck, he answers the enemy with a shot and hits him with a probability of 0.3. If a
not struck, he answers the enemy with a shot and hits him with a probability of 0.3. If a  this shot is not struck, then he does by
this shot is not struck, then he does by  his last shot, which hits him with a probability of 0.4. Find the probability that the battle will be hit: a) party
his last shot, which hits him with a probability of 0.4. Find the probability that the battle will be hit: a) party  b) participant
b) participant  .
.
Decision. Consider the events:
 - member loss
- member loss  ,
,
 - member loss
- member loss  .
.
To perform the event  It is necessary to combine (product) two events: 1)
It is necessary to combine (product) two events: 1)  didn't hit
didn't hit  first shot and 2)
first shot and 2)  struck and his return shot. By the probability multiplication theorem, we obtain
struck and his return shot. By the probability multiplication theorem, we obtain
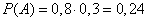 .
.
Go to the event  . It obviously consists of two incompatible options:
. It obviously consists of two incompatible options:
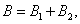
Where 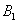 - member loss
- member loss  first shot
first shot  ,
, 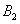 - member loss
- member loss  second shot
second shot  .
.
By the addition theorem
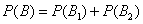 .
.
By condition 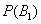 = 0.2. As for the event
= 0.2. As for the event 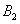 then it is a combination (product) of three events, namely:
then it is a combination (product) of three events, namely:
1) first side shot  should not hit
should not hit  ;
;
2) side response shot  should not hit
should not hit  ;
;
3) the last (second) side shot  must hit
must hit  .
.
By the probability multiplication theorem
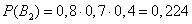 ,
,
from where
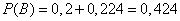 .
.
Example 7. The target, which is being fired, consists of three parts of different vulnerability. To hit a target, one hit in the first part, or two hits in the second, or three hits in the third. If the projectile hit the target, then the probability of it getting into one or another part is proportional to the area of this part. On the projection of the target on a plane perpendicular to the direction of shooting, the first, second and third parts occupy relative areas of 0.1, 0.2 and 0.7. It is known that exactly two shells hit the target. Find the probability that the target will be hit.
Decision. Denote  - defeat the purpose;
- defeat the purpose; 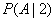 - conditional probability of hitting the target, provided that it hit exactly two shells. Two projectiles that hit the target can hit it in two ways: either at least one of them gets into the first part, or both shells hit the second. These options are incompatible, since only two shells hit the target; therefore, the addition theorem can be applied. The probability that at least one projectile falls into the first part can be calculated through the probability of the opposite event (none of the two projectiles will fall into the first part) and be equal to
- conditional probability of hitting the target, provided that it hit exactly two shells. Two projectiles that hit the target can hit it in two ways: either at least one of them gets into the first part, or both shells hit the second. These options are incompatible, since only two shells hit the target; therefore, the addition theorem can be applied. The probability that at least one projectile falls into the first part can be calculated through the probability of the opposite event (none of the two projectiles will fall into the first part) and be equal to 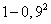 . The probability that both shells fall into the second part is equal to
. The probability that both shells fall into the second part is equal to 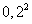 . Consequently,
. Consequently,
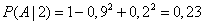 .
.
Example 8. For the conditions of the previous example, find the probability of hitting the target, if it is known that three shells hit it.
Decision. We solve the problem in two ways: through a direct and opposite event.
A direct event — the defeat of a target with three hits — splits into four incompatible options:
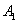 - at least one hit in the first part,
- at least one hit in the first part,
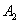 - two hits in the second part and one - in the third,
- two hits in the second part and one - in the third,
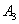 - three hits in the second part,
- three hits in the second part,
 - three hits in the third part.
- three hits in the third part.
The probability of the first option is found as in the previous example:
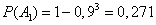 .
.
Find the probability of the second option. Three projectile hit can be distributed in the second and third parts as needed (two to the second and one to the third) in three ways (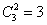 ). Consequently,
). Consequently,
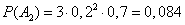 .
.
Next, we find:
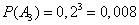 ,
,
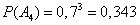 .
.
From here
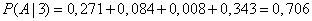 .
.
However, it is easier to solve the problem, if we go to the opposite event - failure to hit the target with three hits. This event can be realized only in one way: if two projectiles out of three fall into the third part, and one into the second. There may be three such combinations ( 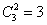 ), therefore
), therefore
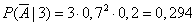 ,
,
from where
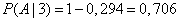 .
.
Example 9. A coin is thrown 6 times. Find the probability that more coats of arms will fall out than numbers.
Decision.To find the probability of an event of interest to us  (more coats of arms will fall out than numbers) it would be possible to list all its possible variants, for example:
(more coats of arms will fall out than numbers) it would be possible to list all its possible variants, for example:
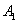 - six emblems and not a single number will appear,
- six emblems and not a single number will appear,
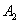 - five coats of arms and one figure will be drawn
- five coats of arms and one figure will be drawn
etc.
However, it will be easier to apply another technique. We list all possible outcomes of the experiment:
 - more coats of arms will fall out than numbers
- more coats of arms will fall out than numbers
 - there will be more figures than emblems,
- there will be more figures than emblems,
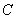 - the same number of figures and coats of arms will appear.
- the same number of figures and coats of arms will appear.
Developments  ,
,  ,
, 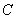 incompatible and form a complete group. Consequently,
incompatible and form a complete group. Consequently,
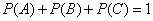 .
.
Since the task is symmetrical with respect to the “coat of arms” and “numbers”,
 ,
,
from where
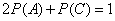
and
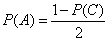 .
.
Let us find the probability of an event 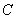 consisting in the fact that with six throwing of a coin, exactly three coats of arms will appear (and, therefore, exactly three digits). The probability of any of the variants of the event
consisting in the fact that with six throwing of a coin, exactly three coats of arms will appear (and, therefore, exactly three digits). The probability of any of the variants of the event 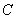 (for example, the sequence g, c, g, g, c, c with six throws) is the same and is equal to
(for example, the sequence g, c, g, g, c, c with six throws) is the same and is equal to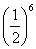 .The number of such combinations is equal to
.The number of such combinations is equal to 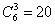 (the number of ways, from which it is possible to choose from six throws three, in which the coat of arms appeared). Consequently,
(the number of ways, from which it is possible to choose from six throws three, in which the coat of arms appeared). Consequently,
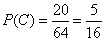 ;
;
from here
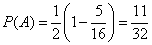 .
.
Пример 10. Прибор состоит из четырех узлов: 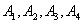 , причем узел
, причем узел 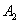 дублирует узел
дублирует узел 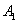 , а узел
, а узел  дублирует узел
дублирует узел 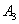 . При отказе (выходе из строя) любого из основных узлов (
. При отказе (выходе из строя) любого из основных узлов ( 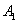 or
or 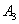 ) происходит автоматическое переключение на дублирующий узел. Надежность (вероятность безотказной работы) в течение заданного времени каждого из узлов равна соответственно
) происходит автоматическое переключение на дублирующий узел. Надежность (вероятность безотказной работы) в течение заданного времени каждого из узлов равна соответственно 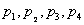 . Надежность каждого из переключающих устройств равна
. Надежность каждого из переключающих устройств равна 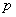 . Все элементы выходят из строя независимо друг от друга. Определить надежность прибора.
. Все элементы выходят из строя независимо друг от друга. Определить надежность прибора.
Decision. Рассмотрим совокупность узлов 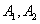 и соответствующего переключающего устройства как один «обобщенный узел»
и соответствующего переключающего устройства как один «обобщенный узел»  , а совокупность узлов
, а совокупность узлов 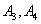 и соответствующего обобщающего устройства – как обобщенный узел
и соответствующего обобщающего устройства – как обобщенный узел 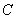 . Consider the events:
. Consider the events:
 – безотказная работа прибора,
– безотказная работа прибора,
 – безотказная работа обобщенного узла
– безотказная работа обобщенного узла  ,
,
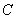 – безотказная работа обобщенного узла
– безотказная работа обобщенного узла 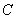 .
.
Obviously
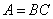 ,
,
from where
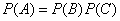 .
.
Find the probability of the event  . It falls into two variants:
. It falls into two variants:
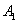 - the node worked properly
- the node worked properly 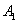
and
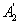 - the node
- the node 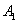 failed, but the switching device and the node turned out to be serviceable
failed, but the switching device and the node turned out to be serviceable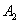 .
.
We have:
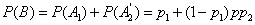 ,
,
similarly
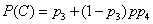 ,
,
from where
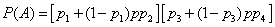 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis