Lecture
When studying systems of random variables, one should always pay attention to the degree and nature of their dependence. This dependence can be more or less pronounced, more or less close. In some cases, the relationship between random variables can be so close that, knowing the value of one random variable, you can accurately specify the value of another. In the other extreme case, the relationship between random variables is so weak and distant that they can practically be considered independent.
The concept of independent random variables is one of the important concepts of probability theory.
Random value  called independent of random variable
called independent of random variable  if the distribution law
if the distribution law  does not depend on what value the value took
does not depend on what value the value took  .
.
For continuous random variables, the condition of independence  from
from  can be written as:
can be written as:
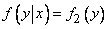
at any 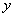 .
.
On the contrary, in case  depends on
depends on  then
then
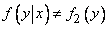 .
.
We prove that the dependence or independence of random variables is always reciprocal: if the value  does not depend on
does not depend on  .
.
Indeed let  does not depend on
does not depend on  :
:
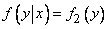 . (8.5.1)
. (8.5.1)
From formulas (8.4.4) and (8.4.5) we have:
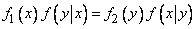 ,
,
from which, taking into account (8.5.1), we obtain:
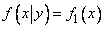
Q.E.D.
Since the dependence and independence of random variables are always reciprocal, a new definition of independent random variables can be given.
Random variables  and
and  are called independent if the distribution law of each of them does not depend on what value the other takes. Otherwise the values
are called independent if the distribution law of each of them does not depend on what value the other takes. Otherwise the values  and
and  are called dependent.
are called dependent.
For independent continuous random variables, the multiplication theorem for the distribution laws takes the form:
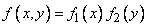 , (8.5.2)
, (8.5.2)
that is, the distribution density of a system of independent random variables is equal to the product of the distribution densities of the individual variables in the system.
Condition (8.5.2) can be considered as a necessary and sufficient condition for the independence of random variables.
Often by the very sight of the function 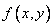 it can be concluded that random variables
it can be concluded that random variables  ,
,  are independent, namely if the distribution density
are independent, namely if the distribution density 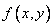 splits into the product of two functions, of which one depends only on
splits into the product of two functions, of which one depends only on 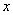 the other is only from
the other is only from 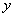 , then the random variables are independent.
, then the random variables are independent.
Example. System density 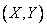 has the form:
has the form:
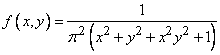 .
.
Determine whether random variables are dependent or independent.  and
and  .
.
Decision. Decomposing the denominator into factors, we have:
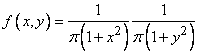 .
.
From what function 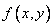 broke up into a product of two functions, one of which is dependent only on
broke up into a product of two functions, one of which is dependent only on 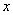 and the other is only from
and the other is only from 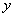 , we conclude that the values
, we conclude that the values  and
and  must be independent. Indeed, applying formulas (8.4.2) and (8.4.3), we have:
must be independent. Indeed, applying formulas (8.4.2) and (8.4.3), we have:
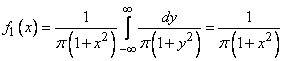 ;
;
similarly
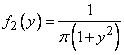 ,
,
how do we make sure that
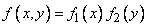
and therefore the values  and
and  are independent.
are independent.
The above criterion for judging the dependence or independence of random variables is based on the assumption that the distribution law of the system is known to us. In practice, the opposite is often the case: the law of distribution of a system  not known; only the laws of the distribution of individual quantities in the system are known, and there is reason to believe that the quantities
not known; only the laws of the distribution of individual quantities in the system are known, and there is reason to believe that the quantities  and
and  are independent. Then you can write the distribution density of the system as the product of the distribution densities of the individual quantities in the system.
are independent. Then you can write the distribution density of the system as the product of the distribution densities of the individual quantities in the system.
Let us dwell in more detail on the important concepts of "dependence" and "independence" of random variables.
The concept of “independence” of random variables, which we use in probability theory, is somewhat different from the usual concept of “dependence” of quantities, which we operate in mathematics. Indeed, usually by “dependency” of quantities one means only one type of dependency - a complete, rigid, so-called — functional dependency. Two values  and
and  They are called functionally dependent if, knowing the value of one of them, you can accurately indicate the value of the other.
They are called functionally dependent if, knowing the value of one of them, you can accurately indicate the value of the other.
In the theory of probability, we encounter another, more general, type of dependence — with probabilistic or “stochastic” dependence. If the value  is related to the value
is related to the value  probabilistic dependence, then, knowing the value
probabilistic dependence, then, knowing the value  , you can not specify the exact value
, you can not specify the exact value  , and you can specify only its distribution law, depending on what value the value took
, and you can specify only its distribution law, depending on what value the value took  .
.
Probabilistic dependence may be more or less close; with increasing closeness of probabilistic dependence, it is increasingly approaching the functional one. Thus, the functional dependence can be considered as an extreme, limiting case of the closest probabilistic dependence. Another extreme case is the complete independence of random variables. Between these two extreme cases lie all gradations of probabilistic dependence - from the strongest to the weakest. Those physical quantities that we consider functionally dependent in practice are in fact closely related to a very close probabilistic dependence: for a given value of one of these quantities, the other fluctuates in such narrow limits that it can practically be considered quite definite. On the other hand, those values that we consider independent in practice, and reality are often in some kind of interdependence, but this dependence is so weak that it can be neglected for practical purposes.
Probabilistic dependence between random variables is very often found in practice. If random values  and
and  are in probabilistic dependence, it does not mean that with a change in the magnitude
are in probabilistic dependence, it does not mean that with a change in the magnitude  magnitude
magnitude  changes in a very specific way; it only means that with changing magnitude
changes in a very specific way; it only means that with changing magnitude  magnitude
magnitude  also tends to change (for example, to increase or decrease with increasing
also tends to change (for example, to increase or decrease with increasing  ). This tendency is observed only “on average”, in general, and in each individual case deviations from it are possible.
). This tendency is observed only “on average”, in general, and in each individual case deviations from it are possible.
Consider, for example, two such random variables:  - growth at random taken person
- growth at random taken person  - its weight. Obviously the magnitude
- its weight. Obviously the magnitude  and
and  are in a certain probability relationship; it is expressed in the fact that in general, people with greater growth have more weight. You can even make an empirical formula that approximately replaces this probabilistic dependence of the functional. Such, for example, is the well-known formula, approximately expressing the relationship between height and weight:
are in a certain probability relationship; it is expressed in the fact that in general, people with greater growth have more weight. You can even make an empirical formula that approximately replaces this probabilistic dependence of the functional. Such, for example, is the well-known formula, approximately expressing the relationship between height and weight:
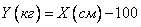 .
.
Formulas of this type are obviously not exact and express only a certain average, mass regularity, a tendency from which deviations are possible in each individual case.
In the above example, we dealt with a case of explicit dependence. Now consider these two random variables:  - growth at random taken person;
- growth at random taken person; 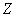 - his age. Obviously, for an adult size
- his age. Obviously, for an adult size  and
and 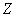 can be considered practically independent; on the contrary, for a child of magnitude
can be considered practically independent; on the contrary, for a child of magnitude  and
and 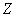 are addicted.
are addicted.
Let us give some more examples of random variables that are in various degrees of dependence.
1. Of the stones that make up the pile of rubble, one stone is selected at random. Random value 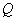 - the weight of the stone; random value
- the weight of the stone; random value 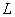 - the greatest length of the stone. Values
- the greatest length of the stone. Values 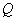 and
and 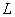 are explicitly probabilistic dependence.
are explicitly probabilistic dependence.
2. Shooting a rocket at a predetermined area of the ocean. Magnitude 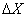 - longitudinal error of the point of impact (undershoot, flight); random value
- longitudinal error of the point of impact (undershoot, flight); random value 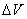 - error in the rocket speed at the end of the active part of the movement. Values
- error in the rocket speed at the end of the active part of the movement. Values 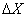 and
and 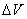 obviously dependent because the error
obviously dependent because the error 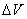 is one of the main reasons for the longitudinal error
is one of the main reasons for the longitudinal error 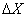 .
.
3. The aircraft, while in flight, measures the height above the Earth's surface using a barometric instrument. Two random variables are considered: 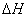 - height measurement error and
- height measurement error and 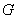 - weight of fuel remaining in the fuel tanks at the time of measurement. Values
- weight of fuel remaining in the fuel tanks at the time of measurement. Values 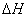 and
and 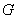 can practically be considered independent.
can practically be considered independent.
In the next  we will get acquainted with some numerical characteristics of a system of random variables, which will enable us to estimate the degree of dependence of these quantities.
we will get acquainted with some numerical characteristics of a system of random variables, which will enable us to estimate the degree of dependence of these quantities.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis