Bertrand Paradox (probability)

Bertrand's paradox is the problem of the classical definition of probability theory. Joseph Bertrand described a paradox in his work Calcul des probabilités (1888) as an example of the fact that probability cannot be clearly defined until the mechanism or method for choosing a random variable is defined ^[1] .

Bertrand's wording [edit]

Bertrand's paradox is this: consider an equilateral triangle inscribed in a circle. A chord of a circle is chosen at random. What is the probability that the selected chord is longer than the side of the triangle?

Bertrand proposed three solutions, apparently correct, but giving different results.

1. 

   Random chords selected by method 1; red - longer than the side of the triangle, blue - shorter
   The method of "random ends": at random, choose two points on the circle and draw a chord through them. To calculate the desired probability, imagine that the triangle is rotated so that one of its vertices coincides with the end of the chord. Note that if the other end of the chord lies on the arc between the two other vertices of the triangle, then the length of the chord is greater than the side of the triangle. The length of the considered arc is equal to one third of the circumference, following the classical definition, the desired probability is equal to .
2. 

   Random chords selected by method 2
   The method of "random radius": fix the radius of the circle, at random, choose a point on the radius. Construct a chord perpendicular to the fixed radius passing through the selected point. To find the desired probability, imagine that the triangle is rotated so that one of its sides is perpendicular to the fixed radius. The chord is longer than the side of the triangle if its center is closer to the center than the intersection point of the triangle with a fixed radius. The side of the triangle halves the radius, hence the probability to choose a chord longer than the side of the triangle .
3. 

   Random chords selected by method 3
   The “random center” method: select at random an arbitrary point inside the circle and construct a chord with center at the selected point. The chord is longer than the side of an equilateral triangle if the selected point is inside a circle inscribed in a triangle. The area of ​​the inscribed circle is 1/4 of the area larger, which means the initial probability is equal to .
   
   

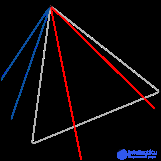
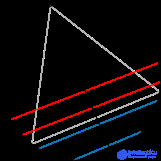
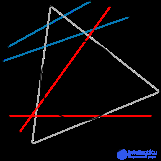
The choice of method can also be depicted as follows. The chord is uniquely given by its middle. All three methods described above give a different, each its own, distribution of the middle. Methods 1 and 2 represent two different non-uniform distributions, while the third method gives a uniform distribution. On the other hand, if you look at the images of the chords below, it is noticeable that the chords in method 2 give a uniformly filled circle, and the 1st and 3rd methods do not give such a picture.

The midpoints of the chord are randomly selected. Method 1	The midpoints of the chord are randomly selected. Method 2	The midpoints of the chord are randomly selected. Method 3
Randomly selected chords. Method 1	Randomly selected chords. Method 2	Randomly selected chords. Method 3

Other distributions may be invented; many of them will give different shares of chords that are longer than the side of the inscribed triangle.

Classic solution [edit]

The classical solution to the problem, therefore, depends on the method by which the chord is randomly chosen. If and only if the method of random selection is given, the problem has a clearly defined solution. The selection method is not unique, so there can be no one solution. The three solutions presented by Bertrand correspond to different selection methods, and in the absence of additional information there is no reason to prefer any one.

This and other paradoxes of the classical definition of probability justify more rigorous formulations, including frequency probabilities and subjective Bayesian probabilities.

Jane's decision using the uncertainty principle [edit]

Edwin Janes, in his 1973 work “The Right Problem” ^[2] proposed a solution to the Bertrand paradox based on the principle of uncertainty: we should not use information that is not given in the condition. Jaynes pointed out that the Bertrand problem did not specify the position or size of the circle, and argued that in this case any exact and objective solutions should be “indifferent” to size and position. In other words, the solution must be invariant to size and transformation.

To illustrate: for example, chords randomly lie in a circle with a diameter of 2 (say, after having straws thrown into a circle from a distance). Then another circle with a smaller diameter (for example, 1.1) is superimposed on the larger one. Now the distribution of chords in a smaller circle should be the same as in a larger one. If you move a smaller circle on a larger one, the probability should not change. This should be clearly expressed in case of changes in method 3: the distribution of chords in a small circle may look qualitatively different than their distribution in a large circle.

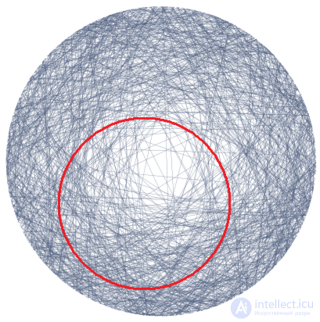
The same situation with method 1, although it is more complex in a graphic image. The only method 2 is invariant both dimensionally and transformationally, method 3 has only dimensional invariance, method 1 - none.

However, Jaynes did not only use invariance to accept or reject these methods: it would mean the same thing as to leave the possibility of the existence of a method that has not yet been described that meets the criteria of common sense. Jains used integral equations, describing invariance, to accurately determine the probability of distribution. For this problem, the integral equalities really have a unique solution - that which is called above method 2, the method of random radius.

Physical experiments [edit]

Method 2 is the only solution with transformational invariance, which is present in certain physical systems (such as statistical mechanics and gas physics), as well as in the experiment proposed by James with the occasional throwing of straws from a distance into a circle. However, someone may conduct other experiments that produce results regarding other methods. For example, in order to arrive at a solution in method 1, the method of random ends, you can attach a rotator to the center of a circle and allow the results of two independent rotations to mark the end points of the chords. In order to come to a solution in method 3, you need to cover the circle with molasses and mark the first point where the middle point of the chord will land. Several observers have developed experiments to obtain various solutions and verify the results empirically. ^{[3] [4] [5]}