Coefficient of determination

Determination coefficient ( 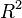- R-squared ) is the fraction of the variance of the dependent variable explained by the dependency model in question, that is, the explanatory variables. More precisely, it is one minus the share of unexplained variance (variance of the random model error, or conditional on the variance factors of the dependent variable) in the variance of the dependent variable. It is considered as a universal measure of the dependence of one random variable on many others. In the particular case of linear dependence 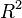is the square of the so-called multiple correlation coefficient between the dependent variable and explanatory variables. In particular, for the paired linear regression model, the coefficient of determination is equal to the square of the normal correlation coefficient between y and x .

Definition and Formula [edit]

The true coefficient of determination of the model of the dependence of the random variable y on the factors x is determined as follows:

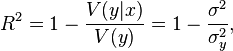
Where 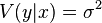- conditional (in terms of x factors) variance of the dependent variable (variance of the random error of the model).

This definition uses true parameters characterizing the distribution of random variables. If we use the sample estimate of the values ​​of the corresponding variances, then we obtain the formula for the sample coefficient of determination (which is usually meant by the coefficient of determination):

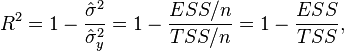
Where 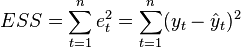- the sum of the squares of the regression residuals, 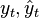- actual and calculated values ​​of the explained variable.

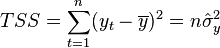- total sum of squares.

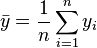
In the case of linear regression with a constant 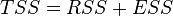where 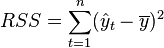- explained sum of squares, so we get a simpler definition in this case - the coefficient of determination is the proportion of the sum of squares explained in the total :

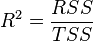
It should be emphasized that this formula is valid only for the model with a constant; in general, it is necessary to use the previous formula.

Interpretation [edit]

1. The coefficient of determination for a model with a constant takes values ​​from 0 to 1. The closer the value of the coefficient to 1, the stronger the dependence. When evaluating regression models, this is interpreted as matching the model with the data. For acceptable models, it is assumed that the coefficient of determination should be at least not less than 50% (in this case, the multiple correlation coefficient exceeds 70% in absolute value). Models with a coefficient of determination above 80% can be considered quite good (the correlation coefficient exceeds 90%). The value of the coefficient of determination 1 means the functional dependence between variables.
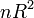2. In the absence of a statistical relationship between the explained variable and factors, the statistics for linear regression has an asymptotic distribution 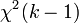where 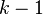- the number of factors of the model (see the test of Lagrange multipliers). In the case of linear regression with normally distributed random errors, the statistics 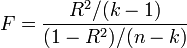has an exact (for samples of any size) Fisher distribution 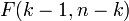(see F-test). Information about the distribution of these values ​​allows you to check the statistical significance of the regression model based on the value of the coefficient of determination. In fact, in these tests the hypothesis about the equality of the true coefficient of determination to zero is checked.
3. In the general case, the coefficient of determination can be negative, which indicates the extreme inadequacy of the model: a simple average approximates better.

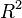Disadvantage and alternative indicators [edit]

The main problem of application (selective) 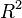is that its value increases ( does not decrease) from adding new variables to the model, even if these variables have nothing to do with the explained variable! Therefore, the comparison of models with different numbers of factors using the coefficient of determination, generally speaking, is incorrect. For these purposes, you can use alternative indicators.

Adjusted [edit]

In order to be able to compare models with different numbers of factors so that the number of regressors (factors) does not affect the statistics 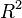commonly used is the corrected coefficient of determination , which uses unbiased estimates of variances:

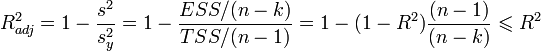
which gives a penalty for additionally included factors, where n is the number of observations, and k is the number of parameters.

This indicator is always less than one, but theoretically it can be less than zero (only with a very small value of the usual coefficient of determination and a large number of factors). Therefore, the interpretation of the indicator as a “share” is lost. However, the use of the indicator in the comparison is justified.

For models with the same dependent variable and the same sample size, comparing models using the adjusted coefficient of determination is equivalent to comparing them using the residual variance 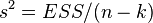or standard model error . The only difference is that the latter criteria the smaller the better.

Information criteria [edit]

AIC , the Akaike information criterion, is used exclusively for comparing models. The lower the value, the better. Often used to compare time series models with different numbers of lags.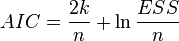
where k is the number of model parameters.
BIC or SC - Bayesian Schwarz Information Criterion - is used and interpreted in the same way as AIC.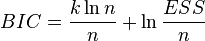
. Gives a greater penalty for the inclusion of extra lags in the model than the AIC.

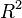-shared (extended) [edit]

In the absence of a regression in a linear multiple OLS, the constant of the property of the coefficient of determination may be violated for a particular implementation. Therefore, regression models with and without a free member cannot be compared by the criterion 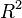. This problem is solved by constructing a generalized coefficient of determination. 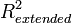, which coincides with the initial one for the case of OLS regression with a free member, and for which the four properties listed above are satisfied. The essence of this method is to consider the projection of the unit vector onto the plane of explanatory variables.

For a regression case without a free member: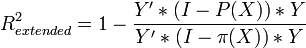
,
where X is the nxk matrix of factor values, 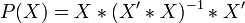- a projector on the X plane, 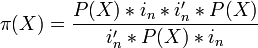where 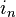- the unit vector nx1.

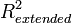with the condition of a small modification , it is also suitable for comparison between the regressions constructed using: OLS, generalized least squares method (OMNK), conditional least squares method (UMNKs), generalized conditional least squares method (OMKN).

Note [edit]

High values ​​of the coefficient of determination, generally speaking, do not indicate the presence of a causal relationship between the variables (as well as in the case of the usual correlation coefficient). For example, if the explained variable and factors that are not actually associated with the explained variable have increasing dynamics, then the coefficient of determination will be quite high. Therefore, the logical and semantic adequacy of the model are of paramount importance. In addition, it is necessary to use criteria for a comprehensive analysis of the quality of the model.

See also [edit]

• Correlation coefficient
• Correlation
• Multicollinearity
• Random Variance
• The method of group accounting of arguments
• Regression analysis

Notes [edit]