Lecture
Let be 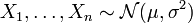 - independent sampling from the normal distribution, where
- independent sampling from the normal distribution, where 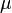 - known mean. Define arbitrary
- known mean. Define arbitrary 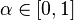 and build
and build 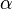 - confidence interval for unknown dispersion
- confidence interval for unknown dispersion 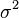 .
.
Statement. Random value
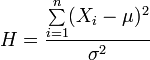
has a distribution  . Let be
. Let be 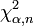 -
- 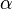 -quantile of this distribution. Then we have:
-quantile of this distribution. Then we have:
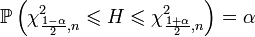 .
. After substitution of the expression for 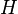 and simple algebraic transformations we get:
and simple algebraic transformations we get:
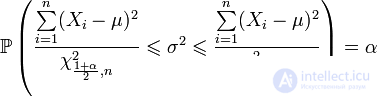 .
. Let be 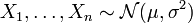 - independent sampling from the normal distribution, where
- independent sampling from the normal distribution, where 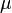 ,
, 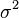 - unknown constants. Construct a confidence interval for the unknown variance
- unknown constants. Construct a confidence interval for the unknown variance 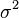 .
.
Fisher's theorem for normal samples. Random value
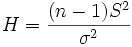 ,
, Where 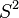 - unbiased sample variance, has a distribution
- unbiased sample variance, has a distribution 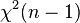 . Then we have:
. Then we have:
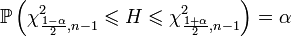 .
. After substitution of the expression for 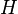 and simple algebraic transformations we get:
and simple algebraic transformations we get:
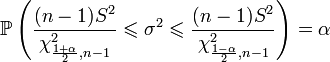 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis