Lecture
One of the most common forms of the central limit theorem was proved by A. M. Lyapunov in 1900. To prove this theorem, A. M. Lyapunov created a special method of characteristic functions. In the future, this method acquired an independent meaning and turned out to be a very powerful and flexible method, suitable for solving various probabilistic problems.
Characteristic function of a random variable 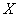 called function
called function
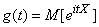 , (13.7.1)
, (13.7.1)
Where 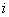 - imaginary unit. Function
- imaginary unit. Function 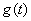 is the mathematical expectation of some complex random variable
is the mathematical expectation of some complex random variable
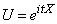 ,
,
functionally related to the value 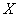 . When solving many problems of probability theory, it is more convenient to use characteristic functions than the laws of distribution.
. When solving many problems of probability theory, it is more convenient to use characteristic functions than the laws of distribution.
Knowing the distribution law of a random variable 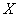 , it is easy to find its characteristic function.
, it is easy to find its characteristic function.
If a 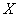 - discontinuous random variable with a number of distribution
- discontinuous random variable with a number of distribution
|
|
|
|
|
|
|
|
|
|
then its characteristic function
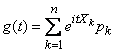 (13.7.2)
(13.7.2)
If a 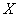 - continuous random variable with distribution density
- continuous random variable with distribution density 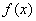 then its characteristic function
then its characteristic function
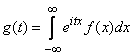 . (13.7.3)
. (13.7.3)
Example 1. Random variable 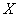 - number of hits with one shot. The probability of hitting is equal to
- number of hits with one shot. The probability of hitting is equal to 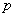 . Find the characteristic function of a random variable
. Find the characteristic function of a random variable 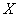 .
.
Decision. By the formula (13.7.2) we have:
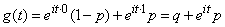 ,
,
Where 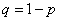 .
.
Example 2. Random variable 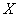 has a normal distribution:
has a normal distribution:
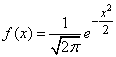 . (13.7.4)
. (13.7.4)
Determine its characteristic function.
Decision. By the formula (13.7.3) we have:
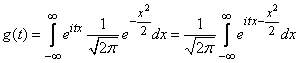 . (13.7.5)
. (13.7.5)
Using the well-known formula
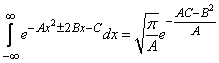
and bearing in mind that 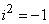 , we get:
, we get:
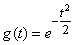 . (13.7.6)
. (13.7.6)
The formula (13.7.3) expresses the characteristic function 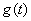 continuous random variable
continuous random variable 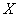 through its distribution density
through its distribution density 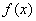 . Transformation (13.7.3) to be subjected
. Transformation (13.7.3) to be subjected 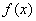 , To obtain
, To obtain 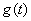 called the Fourier transform. Mathematical analysis courses prove that if a function
called the Fourier transform. Mathematical analysis courses prove that if a function 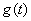 expressed through
expressed through 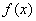 using the Fourier transform, then, in turn, the function
using the Fourier transform, then, in turn, the function 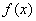 expressed through
expressed through 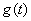 using the so-called inverse Fourier transform:
using the so-called inverse Fourier transform:
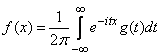 . (13.7.7)
. (13.7.7)
We formulate and prove the main properties of the characteristic functions.
1. If random variables 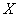 and
and 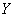 related by
related by
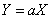 ,
,
Where 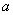 - non-random factor, their characteristic functions are related by:
- non-random factor, their characteristic functions are related by:
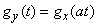 . (13.7.8)
. (13.7.8)
Evidence:
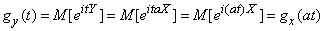 .
.
2. The characteristic function of the sum of independent random variables is equal to the product of the characteristic functions of the terms.
Evidence. Are given  - independent random variables with characteristic functions
- independent random variables with characteristic functions
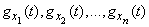
and their sum
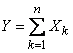 .
.
It is required to prove that
 . (13.7.9)
. (13.7.9)
We have
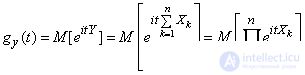 .
.
As magnitudes 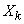 independent, independent and their functions
independent, independent and their functions 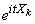 . By the theorem of multiplying the mathematical expectations we get:
. By the theorem of multiplying the mathematical expectations we get:
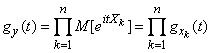 ,
,
Q.E.D.
The apparatus of characteristic functions is often used for the composition of the laws of distribution. Suppose, for example, there are two independent random variables 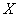 and
and 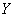 with density distribution
with density distribution 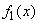 and
and 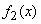 . It is required to find the distribution density
. It is required to find the distribution density
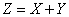 .
.
This can be done as follows: find the characteristic functions 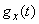 and
and 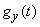 random variables
random variables 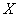 and
and 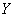 and multiplying them, to obtain the characteristic function of
and multiplying them, to obtain the characteristic function of 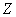 :
:
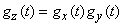 ,
,
after which, subjecting 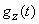 the inverse Fourier transform, find the distribution density
the inverse Fourier transform, find the distribution density 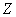 :
:
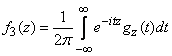 .
.
Example 3. Using the characteristic functions, find the composition of two normal laws:
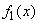 with characteristics
with characteristics 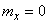 ;
; 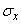 ;
;
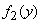 with characteristics
with characteristics 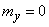 ,
, 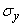 .
.
Decision. Find the characteristic function of 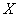 . For this we present it in the form
. For this we present it in the form
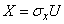 ,
,
Where 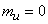 ;
; 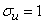 .
.
Using the result of example 2, we find
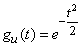 .
.
According to property 1 of the characteristic functions,
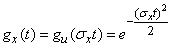 .
.
Similarly
 .
.
Multiplying 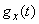 and
and 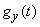 , we have:
, we have:
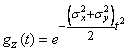 ,
,
and this is the characteristic function of the normal law with parameters 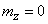 ;
; 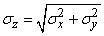 . Thus, the composition of normal laws is obtained by much simpler means than in
. Thus, the composition of normal laws is obtained by much simpler means than in  12.6.
12.6.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis