You get a bonus - 1 coin for daily activity. Now you have 1 coin

13.9. Formulas expressing the central limit theorem and occurring in its practical application

Lecture



According to the central limit theorem, the law of the distribution of a sum of a sufficiently large number of independent random variables (subject to certain non-rigid constraints) is arbitrarily close to normal.

Practically the central limit theorem can be used even when it comes to the sum of a relatively small number of random variables. When summing up independent random variables comparable in their dispersion, with an increase in the number of terms, the law of the distribution of the sum very soon becomes approximately normal. In practice, it is generally widely used approximate replacement of some laws of distribution of others; with the relatively low accuracy required from probabilistic calculations, such a replacement can also be made very approximately. Experience shows that when the number of terms is of the order of ten (and often less), the law of the distribution of the sum can usually be replaced by a normal one.

In practical problems, the central limit theorem is often used to calculate the probability that the sum of several random variables is within the specified limits.

Let be 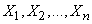13.9. Formulas expressing the central limit theorem and occurring in its practical application - independent random variables with mathematical expectations

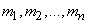
13.9. Formulas expressing the central limit theorem and occurring in its practical application

and dispersions

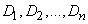13.9. Formulas expressing the central limit theorem and occurring in its practical application .

Suppose that the conditions of the central limit theorem are satisfied (the values 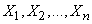13.9. Formulas expressing the central limit theorem and occurring in its practical application comparable in order of their influence on the dispersion of the sum) and the number of terms 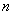13.9. Formulas expressing the central limit theorem and occurring in its practical application enough for the law of distribution of magnitude

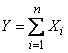13.9. Formulas expressing the central limit theorem and occurring in its practical application (13.9.1)

could be considered approximately normal.

Then the probability that a random variable 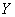13.9. Formulas expressing the central limit theorem and occurring in its practical application falls within the plot 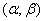13.9. Formulas expressing the central limit theorem and occurring in its practical application expressed by the formula

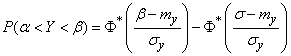13.9. Formulas expressing the central limit theorem and occurring in its practical application , (13.9.2)

Where 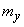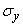13.9. Formulas expressing the central limit theorem and occurring in its practical application , 13.9. Formulas expressing the central limit theorem and occurring in its practical application - expectation and standard deviation of magnitude 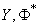13.9. Formulas expressing the central limit theorem and occurring in its practical application - normal distribution function.

According to the theorems of addition of mathematical expectations and variances

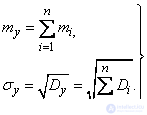13.9. Formulas expressing the central limit theorem and occurring in its practical application (13.9.3)

Thus, in order to approximately find the probabilities of the sum of a large number of random variables falling on a given segment, it is not necessary to know the laws of the distribution of these quantities; it is enough to know only their characteristics. Of course, this applies only to the case when the main condition of the central limit theorem is satisfied - the uniformly small influence of the terms on the dispersion of the sum.

In addition to formulas of the type (13.9.2), in practice, formulas are often used in which instead of the sum of random variables 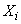13.9. Formulas expressing the central limit theorem and occurring in its practical application their normalized figure appears

13.9. Formulas expressing the central limit theorem and occurring in its practical application . (13.9.4)

Obviously

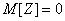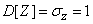13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

If the distribution law 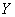13.9. Formulas expressing the central limit theorem and occurring in its practical application close to normal with parameters (13.9.3), then the distribution law 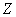13.9. Formulas expressing the central limit theorem and occurring in its practical application close to normal with parameters 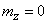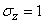13.9. Formulas expressing the central limit theorem and occurring in its practical application , 13.9. Formulas expressing the central limit theorem and occurring in its practical application . From here

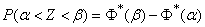13.9. Formulas expressing the central limit theorem and occurring in its practical application . (13.9.5)

Note that the central limit theorem can be applied not only to continuous, but also to discrete random variables, provided that we will operate not with densities, but with distribution functions. Indeed, if the values 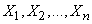13.9. Formulas expressing the central limit theorem and occurring in its practical application discrete, their sum 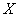13.9. Formulas expressing the central limit theorem and occurring in its practical application - also a discrete random variable and therefore, strictly speaking, cannot obey the normal law. However, all formulas of the type (13.9.2), (13.9.5) remain in force, since they do not include the density, but the distribution function. It can be proved that if discrete random variables satisfy the conditions of the central limit theorem, then the distribution function of their normalized sum 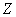13.9. Formulas expressing the central limit theorem and occurring in its practical application (see formula (13.9.4)) when increasing 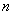13.9. 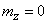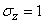Formulas expressing the central limit theorem and occurring in its practical application unboundedly approaches the normal distribution function with parameters 13.9. Formulas expressing the central limit theorem and occurring in its practical application , 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

A special case of the central limit theorem for discrete random variables is the Laplace theorem.

If produced 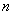13.9. Formulas expressing the central limit theorem and occurring in its practical application independent experiences in each of which the event 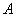13.9. Formulas expressing the central limit theorem and occurring in its practical application appears with probability 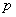13.9. Formulas expressing the central limit theorem and occurring in its practical application then the ratio is fair

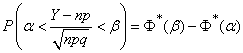13.9. Formulas expressing the central limit theorem and occurring in its practical application , (13.9.6)

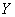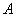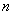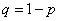Where 13.9. Formulas expressing the central limit theorem and occurring in its practical application - the number of occurrences 13.9. Formulas expressing the central limit theorem and occurring in its practical application at 13.9. Formulas expressing the central limit theorem and occurring in its practical application experiences, 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

Evidence. Let produced 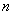13.9. Formulas expressing the central limit theorem and occurring in its practical application independent experiments, in each of which with probability 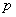13.9. Formulas expressing the central limit theorem and occurring in its practical application event may appear 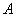13.9. Formulas expressing the central limit theorem and occurring in its practical application . Imagine a random variable. 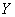13.9. Formulas expressing the central limit theorem and occurring in its practical application - the total number of occurrences of the event in 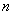13.9. Formulas expressing the central limit theorem and occurring in its practical application experiences - as a sum

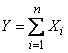13.9. Formulas expressing the central limit theorem and occurring in its practical application , (13.9.7)

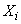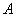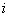Where 13.9. Formulas expressing the central limit theorem and occurring in its practical application - the number of occurrences 13.9. Formulas expressing the central limit theorem and occurring in its practical application at 13.9. Formulas expressing the central limit theorem and occurring in its practical application m experience.

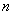According to proven in 13.9. Formulas expressing the central limit theorem and occurring in its practical application 13.8 of the theorem, the distribution law of the sum of identically distributed terms with an increase in their number approaches the normal law. Therefore, with a sufficiently large 13.9. Formulas expressing the central limit theorem and occurring in its practical application the formula (13.9.5) is valid, where

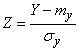13.9. Formulas expressing the central limit theorem and occurring in its practical application . (13.9.8)

AT 13.9. Formulas expressing the central limit theorem and occurring in its practical application 10.3 we proved that the expectation and variance of the number of occurrences of an event in 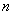13.9. Formulas expressing the central limit theorem and occurring in its practical application independent experiments are equal to:

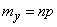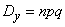
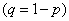13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

Substituting these expressions into (13.9.8), we get

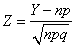13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

and the formula (13.9.5) takes the form:

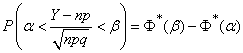13.9. Formulas expressing the central limit theorem and occurring in its practical application .

The theorem is proved.

Example 1. The 100 series of bombs are dropped along the enemy fortifications. When dropping one such series, the expected number of hits is 2, and the standard deviation of the number of hits is 1.5. Approximately find the probability that when dropping 100 episodes from 180 to 220 bombs fall into the lane.

Decision. Imagine the total number of hits as the sum of the numbers of bombs hit in separate series:

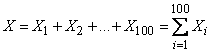13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

Where 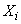13.9. Formulas expressing the central limit theorem and occurring in its practical application - number of hits 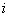13.9. Formulas expressing the central limit theorem and occurring in its practical application th series.

The conditions of the central limit theorem are met, since the values 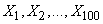13.9. Formulas expressing the central limit theorem and occurring in its practical application equally distributed. We count the number 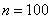13.9. Formulas expressing the central limit theorem and occurring in its practical application sufficient in order to be able to apply the limit theorem (in practice it is usually applicable even for much smaller 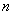13.9. Formulas expressing the central limit theorem and occurring in its practical application ). We have:

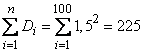13.9. Formulas expressing the central limit theorem and occurring in its practical application , 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

Applying the formula (13.9.6), we get:

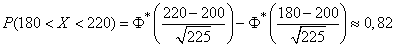13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

that is, with a probability of 0.82, it can be argued that the total number of hits in the band will not go beyond 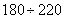13.9. Formulas expressing the central limit theorem and occurring in its practical application .

Example 2. A group air battle occurs in which 50 bombers and 100 fighters participate. Each bomber is attacked by two fighters; Thus, the air combat falls into 50 elementary air battles, each of which involves one bomber and two fighters. In each elementary battle, the probability of shooting down a bomber is 0.4; the probability that both fighters will be shot down in elementary combat is 0.2: the probability that exactly one fighter will be shot down is 0.5. Required: 1) to find the probability that at least 35% of the bombers will be shot down in an air battle; 2) estimate the boundaries in which the number of downed fighters will be concluded with a probability of 0.9.

Decision. 1) denote 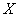13.9. Formulas expressing the central limit theorem and occurring in its practical application - The number of downed bombers;

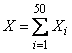13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

Where 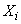13.9. Formulas expressing the central limit theorem and occurring in its practical application - the number of bombers shot down 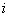13.9. Formulas expressing the central limit theorem and occurring in its practical application m elementary battle.

Distribution range 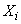13.9. Formulas expressing the central limit theorem and occurring in its practical application has the form:

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

From here

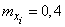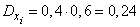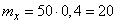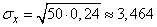13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

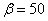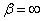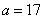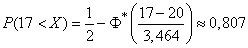Applying the formula (13.9.6) and assuming 13.9. Formulas expressing the central limit theorem and occurring in its practical application (or, equivalently, in this case 13.9. Formulas expressing the central limit theorem and occurring in its practical application ), 13.9. Formulas expressing the central limit theorem and occurring in its practical application , we find:

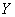13.9. Formulas expressing the central limit theorem and occurring in its practical application .

2) denote 13.9. Formulas expressing the central limit theorem and occurring in its practical application the number of downed fighters:

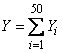13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

Where 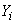13.9. Formulas expressing the central limit theorem and occurring in its practical application - the number of fighters shot down in 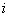13.9. Formulas expressing the central limit theorem and occurring in its practical application m elementary battle.

Distribution range 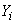13.9. Formulas expressing the central limit theorem and occurring in its practical application has the form:

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

13.9. Formulas expressing the central limit theorem and occurring in its practical application

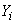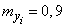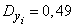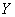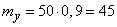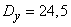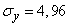From here we find the mathematical expectation and the variance of 13.9. Formulas expressing the central limit theorem and occurring in its practical application :

13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

For size 13.9. Formulas expressing the central limit theorem and occurring in its practical application :

13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application ; 13.9. Formulas expressing the central limit theorem and occurring in its practical application .

Determine the boundaries of the plot, symmetric with respect 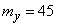13.9. Formulas expressing the central limit theorem and occurring in its practical application to which the value 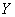13.9. Formulas expressing the central limit theorem and occurring in its practical application . Denote half the length of this section. 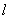13.9. Formulas expressing the central limit theorem and occurring in its practical application . Then

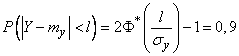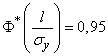13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

13.9. Formulas expressing the central limit theorem and occurring in its practical application .

By function tables 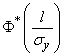13.9. Formulas expressing the central limit theorem and occurring in its practical application find the value of the argument for which 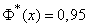13.9. Formulas expressing the central limit theorem and occurring in its practical application ; this value is approximately equal

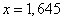13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

those.

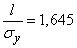13.9. Formulas expressing the central limit theorem and occurring in its practical application ,

from where

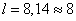13.9. Formulas expressing the central limit theorem and occurring in its practical application .

Consequently, with a probability of about 0.9, it can be argued that the number of downed fighters will be enclosed in the limit 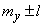13.9. Formulas expressing the central limit theorem and occurring in its practical application , that is, in the range from 37 to 53.

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Probability theory. Mathematical Statistics and Stochastic Analysis

Terms: Probability theory. Mathematical Statistics and Stochastic Analysis