Lecture
The task of determining the distribution law of a function of several random arguments is much more complicated than a similar problem for a function of one argument. Here we present a general method for solving this problem for the simplest case of a function of two arguments.
There is a system of two continuous random variables. 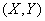 with distribution density
with distribution density 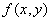 . Random value
. Random value 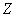 associated with
associated with 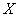 and
and 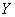 functional dependence:
functional dependence:
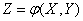 .
.
It is required to find the distribution law 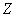 .
.
To solve the problem, we use a geometrical interpretation similar to the one we used in the case of a single argument. Function 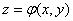 it’s no longer a curve, but a surface (fig. 12.4.1).
it’s no longer a curve, but a surface (fig. 12.4.1).
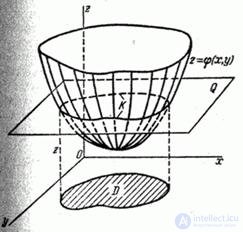
Fig. 12.4.1.
Find the distribution function of 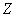 :
:
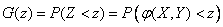 . (12.4.1)
. (12.4.1)
Draw a plane 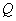 parallel to the plane
parallel to the plane 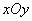 , on distance
, on distance 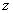 from her. This plane will cross the surface.
from her. This plane will cross the surface. 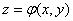 on some curve
on some curve 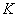 . Design the curve
. Design the curve 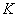 on the plane
on the plane 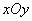 . This projection, whose equation
. This projection, whose equation 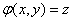 will divide the plane
will divide the plane 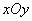 into two areas; for one of them is the height of the surface above the plane
into two areas; for one of them is the height of the surface above the plane 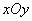 will be less, and for another - more
will be less, and for another - more 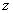 . Denote
. Denote 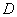 the area for which this height is less
the area for which this height is less 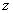 . To satisfy inequality (12.4.1), a random point
. To satisfy inequality (12.4.1), a random point 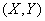 obviously should get into the area
obviously should get into the area  ; Consequently,
; Consequently,
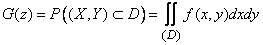 . (12.4.2)
. (12.4.2)
In the expression (12.4.2) value  enters implicitly through the limits of integration.
enters implicitly through the limits of integration.
Differentiating 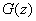 by
by 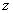 , we obtain the distribution density
, we obtain the distribution density 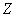 :
:
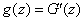 .
.
Knowing the specific type of function 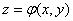 , you can express the limits of integration through
, you can express the limits of integration through 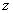 and write the expression
and write the expression 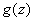 explicitly.
explicitly.
In order to find the distribution law of the function of two arguments, there is no need to construct a surface each time. 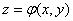 , just as it is done in fig. 12.4.1, and cross it by a plane parallel to
, just as it is done in fig. 12.4.1, and cross it by a plane parallel to 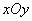 . In practice, it is enough to build on the plane
. In practice, it is enough to build on the plane 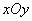 curve whose equation
curve whose equation 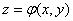 , be aware of which side of this curve
, be aware of which side of this curve 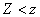 and for what
and for what 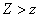 and integrate by region
and integrate by region 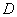 , for which
, for which 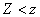 .
.
Example. System of quantities 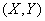 subject to the distribution law with density
subject to the distribution law with density 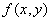 . Magnitude
. Magnitude 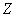 there is a product of quantities
there is a product of quantities 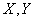 :
:
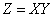 .
.
Find the density distribution 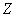 .
.
Decision. Let's set some value 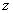 and build on the plane
and build on the plane 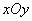 curve whose equation
curve whose equation 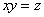 (fig. 12.4.2). This is a hyperbole whose asymptotes coincide with the axes of coordinates. Region
(fig. 12.4.2). This is a hyperbole whose asymptotes coincide with the axes of coordinates. Region 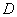 in fig. 12.4.2 shaded.
in fig. 12.4.2 shaded.
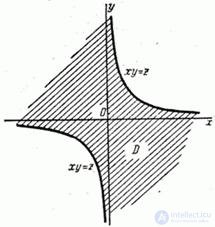
Fig. 12.4.2.
Distribution function of magnitude 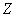 has the form:
has the form:
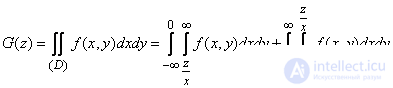 .
.
Differentiating this expression by 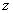 , we have:
, we have:
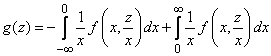 . (12.4.3)
. (12.4.3)
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis