You get a bonus - 1 coin for daily activity. Now you have 1 coin

The addition theorem for probabilities of incompatible events

Lecture



The addition theorem for probabilities of incompatible events

Theorem. Probability of the sum of a finite number of incompatible events The addition theorem for probabilities of incompatible events 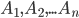equal to the sum of the probabilities of these events 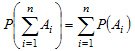The addition theorem for probabilities of incompatible events (2.1)

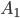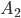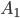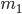Evidence. Let us prove this theorem for the case of the sum of two incompatible events. The addition theorem for probabilities of incompatible events and The addition theorem for probabilities of incompatible events . Let the event The addition theorem for probabilities of incompatible events favor The addition theorem for probabilities of incompatible events elementary outcomes, and event A2: m2 outcomes. 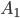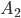Since the events The addition theorem for probabilities of incompatible events and The addition theorem for probabilities of incompatible events according to the condition of the theorem, incompatible, then the A1 + A2 event is favored by m1 + m2 of elementary outcomes from the total number of n outcomes. 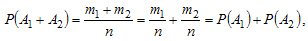Consequently, The addition theorem for probabilities of incompatible events ,

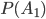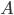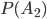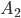Where The addition theorem for probabilities of incompatible events - probability of an event The addition theorem for probabilities of incompatible events ; The addition theorem for probabilities of incompatible events - probability of an event The addition theorem for probabilities of incompatible events .

An example . For shipment from the warehouse can be allocated one of two machines of various types. Known probabilities of highlighting each machine: 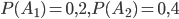The addition theorem for probabilities of incompatible events .

Then the probability of receipt to the warehouse of at least one of these machines will be

P (A 1 + A 2 ) = 0.2 + 0.4 = 0.6.

Conditional probability

In many cases, the probabilities of occurrence of some events depend on whether another event has occurred or not. For example, the probability of timely release of the machine depends on the delivery of components. If these products are already delivered, then the desired probability will be one. If it is determined before the delivery of components, then its value will obviously be different. Event probability 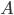The addition theorem for probabilities of incompatible events calculated on condition that another event has occurred 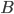The addition theorem for probabilities of incompatible events is called the conditional probability of an event 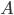The addition theorem for probabilities of incompatible events and is denoted by 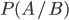The addition theorem for probabilities of incompatible events . 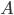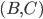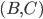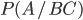In cases where the probability of an event The addition theorem for probabilities of incompatible events considered on condition that two other events occur The addition theorem for probabilities of incompatible events , use conditional probability relative to the product of events The addition theorem for probabilities of incompatible events The addition theorem for probabilities of incompatible events .

Probability multiplication theorem

Theorem. The probability of the product of two events is equal to the product of the probability of one of them by the conditional probability of the other, calculated under the condition that the first took place

P (AB) = P (A) × P (B / A) = P (B) × P (A / B ). (2.2)

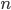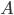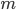Evidence. Suppose that The addition theorem for probabilities of incompatible events all sorts of elementary outcomes event The addition theorem for probabilities of incompatible events favor The addition theorem for probabilities of incompatible events outcomes from which 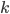The addition theorem for probabilities of incompatible events outcomes favor the event 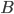The addition theorem for probabilities of incompatible events . 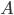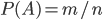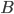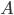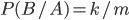Then the probability of an event The addition theorem for probabilities of incompatible events will be The addition theorem for probabilities of incompatible events conditional probability of an event The addition theorem for probabilities of incompatible events regarding the event The addition theorem for probabilities of incompatible events will be The addition theorem for probabilities of incompatible events .

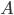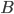The product of events The addition theorem for probabilities of incompatible events and The addition theorem for probabilities of incompatible events only those outcomes favor the event. 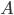The addition theorem for probabilities of incompatible events and event 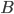The addition theorem for probabilities of incompatible events simultaneously, i.e. 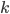The addition theorem for probabilities of incompatible events outcomes. 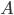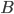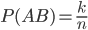Therefore, the probability of an event The addition theorem for probabilities of incompatible events and The addition theorem for probabilities of incompatible events equals The addition theorem for probabilities of incompatible events .

Multiply the numerator and denominator of this fraction by 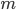The addition theorem for probabilities of incompatible events .

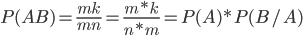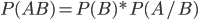Will get The addition theorem for probabilities of incompatible events . The formula is proved similarly. The addition theorem for probabilities of incompatible events .

An example . 35 refrigerators arrived at the warehouse. It is known that 5 refrigerators with defects, but it is unknown what kind of refrigerators it is. Find the probability that two randomly selected coolers will be defective.

Decision. The probability that the first refrigerator selected will be defective is found as the ratio of the number of favorable outcomes to the total number of possible outcomes P (A) = 5/35 = 1/7 . But after the first defective refrigerator was taken, the conditional probability that the second will be defective is determined based on the ratio 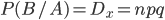The addition theorem for probabilities of incompatible events

The desired probability will be 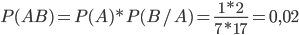The addition theorem for probabilities of incompatible events .

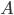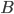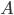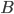If at the occurrence of the event The addition theorem for probabilities of incompatible events event probability The addition theorem for probabilities of incompatible events does not change, then the events The addition theorem for probabilities of incompatible events and The addition theorem for probabilities of incompatible events are called independent . In the case of independent events, the probability of their product is equal to the product of the probabilities of these events.

P (AB) = P (A) × P (B) . (2.3)

The probability multiplication theorem is easily generalized to any finite number of events.

Theorem. The probability of the product of a finite number of events is equal to the product of their conditional probabilities relative to the product of the preceding events, i.e. P (ABC .... LM) = P (A) × P (B / A) × P (C / AB) P (M / AB ... L) . (2.4)

To prove this theorem one can use the method of mathematical induction.

Theorem of addition of joint event probabilities

Two events are called joint , if the appearance of one of them does not exclude the appearance of the other in the same experience. Example. Admission to the store one type of product - the event 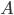The addition theorem for probabilities of incompatible events . Receipt of the second type of product - event 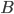The addition theorem for probabilities of incompatible events . These goods can be received simultaneously. 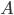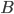therefore The addition theorem for probabilities of incompatible events and The addition theorem for probabilities of incompatible events - joint events.

Theorem. The probability of occurrence of at least one of two joint events is equal to the sum of the probabilities of these events without the probability of their joint occurrence P (A + B) = P (A) + P (B) - P (AB) . (2.5)

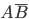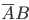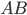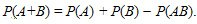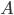Evidence. Event A + B occurs if one of three incompatible events occurs. The addition theorem for probabilities of incompatible events , The addition theorem for probabilities of incompatible events , The addition theorem for probabilities of incompatible events . By the addition theorem of probabilities of incompatible events, we have The addition theorem for probabilities of incompatible events (2.6)

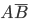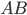Event The addition theorem for probabilities of incompatible events will happen if one of two incompatible events occurs: The addition theorem for probabilities of incompatible events , The addition theorem for probabilities of incompatible events .

Again applying the addition theorem for probabilities of incompatible events, we obtain 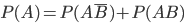The addition theorem for probabilities of incompatible events .

From where

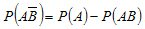The addition theorem for probabilities of incompatible events (2.7)

Similarly for an event

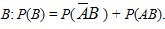
The addition theorem for probabilities of incompatible events

From where 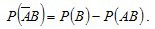The addition theorem for probabilities of incompatible events . (2.8)

Substituting (2.7) and (2.8) into (2.6), we find

P (A + B) = P (A) + P (B) - P (AB) .

Example. If the probability of entry into the store of one type of product is P (A) = 0.4,

and the second commodity, P (B) = 0.5, and if we assume that these events are independent, but are joint, then the probability of the sum of events is

P (A + B) = 0.4 + 0.5 - 0.4 × 0.5 = 0.7 .

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Probability theory. Mathematical Statistics and Stochastic Analysis

Terms: Probability theory. Mathematical Statistics and Stochastic Analysis