Lecture
In a number of areas of practical applications of probability theory (in particular, in the theory of shooting), along with the standard deviation, they often use another characteristic of dispersion, the so-called probable, or median, deviation. Probable deviation is usually indicated by the letter 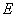 (sometimes B).
(sometimes B).
Probable (median) deviation of a random variable 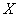 distributed according to the normal law, is called half the length of the section, symmetric about the center of dispersion, the probability of falling into which is equal to half.
distributed according to the normal law, is called half the length of the section, symmetric about the center of dispersion, the probability of falling into which is equal to half.
The geometric interpretation of the probable deviation is shown in Fig. 6.4.1. Probable deviation 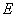 - is half the length of the section of the x-axis, symmetrical with respect to the point
- is half the length of the section of the x-axis, symmetrical with respect to the point 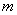 on which half of the distribution curve is based.
on which half of the distribution curve is based.
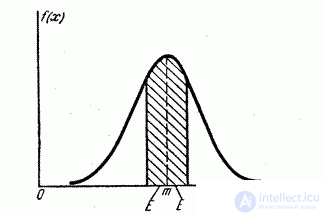
Fig. 6.4.1.
Let us clarify the meaning of the term “median deviation” or “median error”, which is often used in artillery practice instead of “probable deviation”.
Consider a random variable 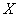 distributed according to normal law. The probability that it deviates from the center of dispersion
distributed according to normal law. The probability that it deviates from the center of dispersion 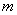 less than
less than 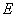 , by definition, the probable deviation
, by definition, the probable deviation 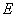 equal to
equal to 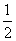 :
:
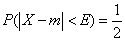 . (6.4.1)
. (6.4.1)
The probability that it deviates from 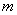 more than
more than 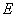 is also equal
is also equal 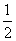 :
:
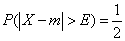 .
.
Thus, with a large number of experiments on average half of the values of the random variable 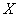 deviate from
deviate from 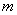 more than
more than 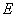 and half less. Hence the term "median error", "median deviation."
and half less. Hence the term "median error", "median deviation."
Obviously, the probable deviation, as a characteristic of dispersion, must be in direct dependence on the standard quadratic deviation 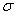 . Calculate the probability of an event
. Calculate the probability of an event 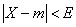 in equation (6.4.1) according to the formula (6.3.10). We have:
in equation (6.4.1) according to the formula (6.3.10). We have:
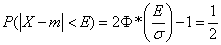 .
.
From here
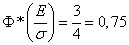 . (6.4.2)
. (6.4.2)
By function tables 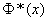 you can find this argument value
you can find this argument value 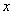 in which it is equal to 0.75. This value is approximately 0.674; from here
in which it is equal to 0.75. This value is approximately 0.674; from here
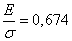 ;
; 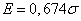 . (6.4.3)
. (6.4.3)
So, knowing the meaning 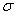 , you can immediately find a proportional value
, you can immediately find a proportional value 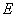 . Often they also use this form of recording this dependence:
. Often they also use this form of recording this dependence:
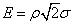 , (6.4.4)
, (6.4.4)
Where 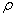 - is the value of the argument in which one of the forms of the probability integral is the so-called Laplace function
- is the value of the argument in which one of the forms of the probability integral is the so-called Laplace function
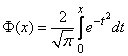
- equal to half. Numerical value 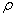 approximately 0.477.
approximately 0.477.
Currently, the probable deviation, as a scattering characteristic, is increasingly being supplanted by a more universal characteristic. 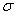 . In a number of areas of applications of the theory of probability, it is preserved only by tradition.
. In a number of areas of applications of the theory of probability, it is preserved only by tradition.
If the probabilistic deviation is taken as the dispersion characteristic 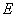 , the density of the normal distribution is written as:
, the density of the normal distribution is written as:
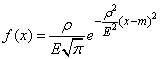 , (6.4.5)
, (6.4.5)
and the probability of getting to the site from 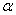 before
before 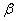 Most often written in the form:
Most often written in the form:
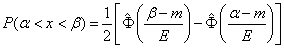 , (6.4.6)
, (6.4.6)
Where
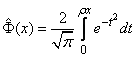 (6.4.7)
(6.4.7)
- the so-called reduced function of Laplace.
Make a calculation similar to that performed in the previous n ° for the standard deviation 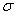 : set aside from the center of dispersion
: set aside from the center of dispersion 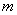 consecutive lengths of one probable deviation
consecutive lengths of one probable deviation 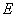 (Fig. 6.4.2) and calculate the probability of falling into these segments with an accuracy of 0.01. We get:
(Fig. 6.4.2) and calculate the probability of falling into these segments with an accuracy of 0.01. We get:
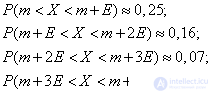
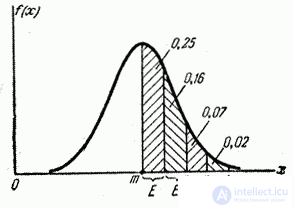
Fig. 6.4.2.
This shows that, with an accuracy of 0.01, all values of a normally distributed random variable are stacked on a plot. 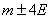 .
.
Example. The attack aircraft produces shelling of a column of enemy troops, whose width is equal to 8 m. The flight is along the column; due to slip there is a systematic error: 2 m to the right in the direction of flight. Main probable deviations: in the direction of flight 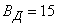 m, in the lateral direction
m, in the lateral direction 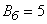 m. Without having at his disposal any probability integral tables, but knowing only numbers:
m. Without having at his disposal any probability integral tables, but knowing only numbers:
25%, 16%, 7%, 2%,
roughly estimate the probability of hitting the convoy with one shot and the probability of at least one hit with three independent shots.
Decision. To solve the problem, it suffices to consider one coordinate of the point of impact - the abscissa. 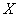 in the direction perpendicular to the column. This abscissa is normally distributed with a center of dispersion.
in the direction perpendicular to the column. This abscissa is normally distributed with a center of dispersion. 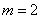 and probable deviation
and probable deviation 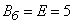 (m) Let us mentally put off segments of 5 m length to the one and the other side from the center of scattering. To the right of the center of scattering, the target occupies a segment of 2 m, which is 0.4 probable deviations. The probability of hitting this site is approximately equal to:
(m) Let us mentally put off segments of 5 m length to the one and the other side from the center of scattering. To the right of the center of scattering, the target occupies a segment of 2 m, which is 0.4 probable deviations. The probability of hitting this site is approximately equal to:
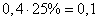 .
.
To the left of the center of dispersion, the target occupies a 6 m section. This is an integer probable deviation (5 m), the probability of hitting it is 25% plus a 1 m length of the next (second from the center) possible deviation, the probability of hitting it is 16%. The probability of hitting a part of 1 m in length is approximately equal to:
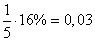 .
.
Thus, the probability of entering the column is approximately equal to:
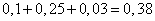 .
.
The probability of at least one hit with three shots is equal to:
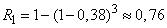
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis