Lecture
Probability function 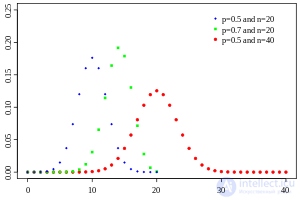 | |
| Distribution function | |
| Designation | 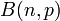 |
| Options | 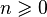 - the number of "tests" - the number of "tests" 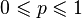 - the probability of "success" - the probability of "success" |
| Carrier | 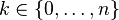 |
| Probability function | 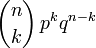 |
| Distribution function | 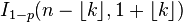 |
| Expected value | 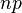 |
| Median | one of 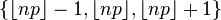 |
| Fashion | 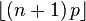 |
| Dispersion |  |
| Asymmetry coefficient | 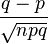 |
| Coefficient of kurtosis | 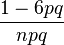 |
| Informational entropy | 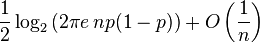 |
| Generating function of moments | 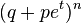 |
| Characteristic function | 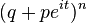 |
The binomial distribution in probability theory is the distribution of the number of “successes” in a sequence of 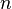 independent random experiments, such that the probability of “success” in each of them is constant and equal
independent random experiments, such that the probability of “success” in each of them is constant and equal 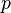 .
.
Let be 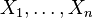 - a finite sequence of independent random variables with the same Bernoulli distribution with the parameter
- a finite sequence of independent random variables with the same Bernoulli distribution with the parameter 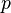 that is, with each
that is, with each 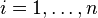 magnitude
magnitude 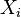 takes values
takes values 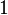 ("Success") and
("Success") and 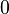 ("Failure") with probabilities
("Failure") with probabilities 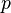 and
and 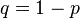 respectively. Then a random variable
respectively. Then a random variable
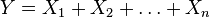
has a binomial distribution with parameters 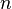 and
and 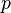 . This is written as:
. This is written as:
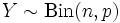 .
. Random variable 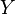 usually interpreted as the number of successes in a series of
usually interpreted as the number of successes in a series of  identical independent Bernoulli tests with probability of success
identical independent Bernoulli tests with probability of success 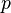 in every test.
in every test.
The probability function is given by the formula:
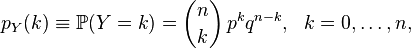
Where
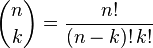 - Binomial coefficient.
- Binomial coefficient. The distribution function of the binomial distribution can be written as a sum:
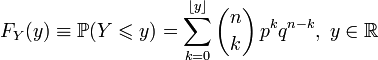 ,
, Where 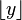 denotes the largest integer not exceeding the number
denotes the largest integer not exceeding the number  , or in the form of an incomplete beta function:
, or in the form of an incomplete beta function:
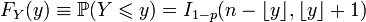 .
. The generating function of moments of the binomial distribution is:
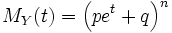 ,
, from where
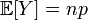 ,
, 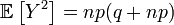 ,
, and the variance is a random variable.
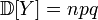 .
. 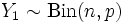 and
and 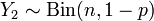 . Then
. Then 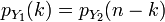 .
. 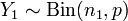 and
and 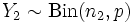 . Then
. Then 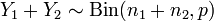 .
. 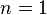 , then, obviously, we obtain the Bernoulli distribution.
, then, obviously, we obtain the Bernoulli distribution. 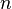 large, then by virtue of the central limit theorem
large, then by virtue of the central limit theorem 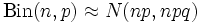 where
where 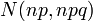 - normal distribution with expectation
- normal distribution with expectation 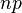 and variance
and variance  .
. 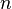 great as well
great as well 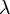 - fixed number, then
- fixed number, then 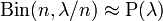 where
where 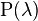 - Poisson distribution with parameter
- Poisson distribution with parameter 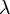 .
. 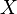 and
and 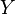 have binomial distributions
have binomial distributions 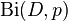 and
and 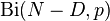 accordingly, the conditional distribution of the random variable
accordingly, the conditional distribution of the random variable 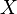 provided
provided 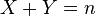 - hypergeometric
- hypergeometric 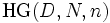 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis