Lecture
In this  we prove one of the simplest, but at the same time the most important forms of the law of large numbers - the Chebyshev theorem. This theorem establishes a connection between the arithmetic mean of the observed values of a random variable and its expectation.
we prove one of the simplest, but at the same time the most important forms of the law of large numbers - the Chebyshev theorem. This theorem establishes a connection between the arithmetic mean of the observed values of a random variable and its expectation.
First we solve the following auxiliary problem.
There is a random variable 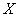 with mathematical expectation
with mathematical expectation 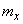 and variance
and variance 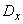 . Above this value is
. Above this value is 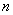 independent experiments and calculates the arithmetic average of all observed values of
independent experiments and calculates the arithmetic average of all observed values of 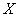 . It is required to find the numerical characteristics of this arithmetic average - the expectation and variance - and find out how they change with increasing
. It is required to find the numerical characteristics of this arithmetic average - the expectation and variance - and find out how they change with increasing 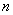 .
.
Denote:
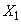 - value
- value 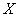 in the first experience;
in the first experience;
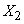 - value
- value 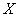 in the second experiment, etc.
in the second experiment, etc.
Obviously, a set of values 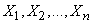 represents
represents 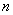 independent random variables, each of which is distributed according to the same law as the quantity itself
independent random variables, each of which is distributed according to the same law as the quantity itself 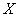 . Consider the arithmetic average of these values:
. Consider the arithmetic average of these values:
 .
.
Random value 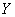 there is a linear function of independent random variables
there is a linear function of independent random variables 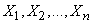 . Find the expectation and variance of this value. According to the rules
. Find the expectation and variance of this value. According to the rules  10 to determine the numerical characteristics of linear functions, we obtain:
10 to determine the numerical characteristics of linear functions, we obtain:
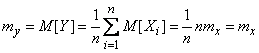 ;
;
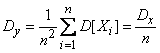 .
.
So, the expected value of 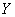 does not depend on the number of experiences
does not depend on the number of experiences 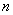 and equal to the expected value of the observed value
and equal to the expected value of the observed value 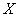 ; as for the variance of magnitude
; as for the variance of magnitude 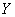 then it decreases unlimitedly with an increase in the number of experiments and with a sufficiently large
then it decreases unlimitedly with an increase in the number of experiments and with a sufficiently large 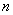 can be made arbitrarily small. We see that the arithmetic mean is a random variable with an arbitrarily small variance and, with a large number of experiments, behaves almost as not random.
can be made arbitrarily small. We see that the arithmetic mean is a random variable with an arbitrarily small variance and, with a large number of experiments, behaves almost as not random.
Chebyshev's theorem establishes in exact quantitative form this property of stability of the arithmetic mean. It is formulated as follows:
With a sufficiently large number of independent experiments, the arithmetic mean of the observed values of a random variable converges in probability to its expected value.
We write the Chebyshev theorem as a formula. For this we recall the meaning of the term "converges in probability." It is said that a random variable 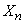 converges in probability to value
converges in probability to value 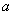 if increasing
if increasing 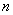 probability that
probability that 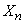 and
and 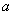 will be arbitrarily close, unlimitedly approaching unity, which means that with a sufficiently large
will be arbitrarily close, unlimitedly approaching unity, which means that with a sufficiently large 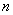
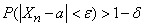 ,
,
Where 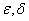 - arbitrarily small positive numbers.
- arbitrarily small positive numbers.
We write in a similar form the Chebyshev theorem. She claims that while increasing 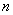 average
average 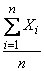 converges in probability to
converges in probability to 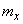 i.e.
i.e.
 . (13.3.1)
. (13.3.1)
Let us prove this inequality.
Evidence. Above it was shown that

has numeric characteristics
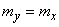 ;
; 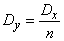 .
.
Apply to random value 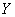 Chebyshev's inequality, believing
Chebyshev's inequality, believing 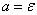 :
:
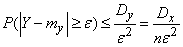 .
.
No matter how small the number 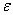 you can take
you can take 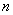 so big that inequality holds
so big that inequality holds
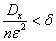
Where 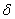 - arbitrarily small number.
- arbitrarily small number.
Then
 ,
,
whence, moving to the opposite event, we have:
 ,
,
Q.E.D.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis