Lecture
Previous 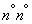 we addressed the issue of estimating an unknown parameter
we addressed the issue of estimating an unknown parameter 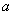 one number. Such an assessment is called "point". In a number of tasks it is required not only to find for the parameter
one number. Such an assessment is called "point". In a number of tasks it is required not only to find for the parameter 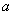 suitable numerical value, but also to assess its accuracy and reliability. It is required to know - to what errors the replacement of the parameter can lead
suitable numerical value, but also to assess its accuracy and reliability. It is required to know - to what errors the replacement of the parameter can lead 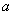 its point estimate
its point estimate 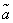 and with what degree of confidence can we expect that these errors will not go beyond certain limits?
and with what degree of confidence can we expect that these errors will not go beyond certain limits?
Such tasks are especially relevant with a small number of observations, when the point estimate 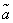 largely random and approximate replacement
largely random and approximate replacement 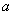 on
on 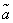 can lead to serious errors.
can lead to serious errors.
To give an idea of the accuracy and reliability of the assessment 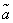 , in mathematical statistics use the so-called confidence intervals and confidence probabilities.
, in mathematical statistics use the so-called confidence intervals and confidence probabilities.
Let for parameter 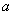 unbiased estimate obtained from experience
unbiased estimate obtained from experience 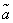 . We want to evaluate the possible error. Assign some fairly large probability
. We want to evaluate the possible error. Assign some fairly large probability 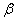 (eg,
(eg, 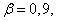
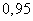 or
or 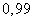 ) such that an event with probability
) such that an event with probability 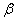 can be considered almost reliable, and find such a value
can be considered almost reliable, and find such a value 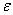 , for which
, for which
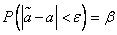 . (14.3.1)
. (14.3.1)
Then the range of practically possible values of the error that occurs when replacing 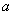 on
on 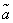 , will be
, will be 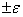 ; large errors in absolute magnitude will appear only with a small probability
; large errors in absolute magnitude will appear only with a small probability 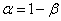 .
.
Rewrite (14.3.1) in the form:
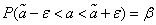 . (14.3.2)
. (14.3.2)
Equality (14.3.2) means that with probability 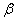 unknown parameter value
unknown parameter value 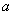 falls into the interval
falls into the interval
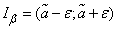 . (14.3.3)
. (14.3.3)
It should be noted one thing. Previously, we have repeatedly considered the probability of a random variable falling into a given non-random interval. Here it is different: the value 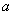 not random, but random
not random, but random 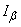 . Randomly its position on the x-axis, determined by its center
. Randomly its position on the x-axis, determined by its center 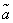 ; the length of the interval is also random
; the length of the interval is also random 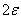 because the magnitude
because the magnitude 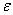 It is calculated, as a rule, by experimental data. Therefore, in this case it is better to interpret the value
It is calculated, as a rule, by experimental data. Therefore, in this case it is better to interpret the value 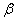 not like the probability of "hitting" the point
not like the probability of "hitting" the point 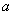 in the interval
in the interval 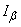 , but as the probability that a random interval
, but as the probability that a random interval 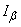 will cover the point
will cover the point 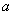 (fig. 14.3.1).
(fig. 14.3.1).
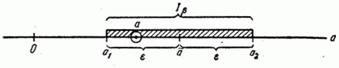
Fig. 14.3.1.
Probability 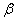 it is accepted to call confidence probability, and the interval
it is accepted to call confidence probability, and the interval 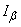 - confidence interval. Interval boundaries
- confidence interval. Interval boundaries 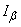 :
: 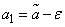 and
and 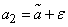 are called confidential boundaries.
are called confidential boundaries.
We give another interpretation of the concept of a confidence interval: it can be considered as an interval of parameter values 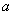 compatible with the experimental data and do not contradict them. Indeed, if we agree to consider an event with probability
compatible with the experimental data and do not contradict them. Indeed, if we agree to consider an event with probability 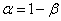 almost impossible then those parameter values
almost impossible then those parameter values 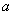 for which
for which 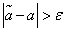 , it is necessary to recognize contradicting experimental data, and those for which
, it is necessary to recognize contradicting experimental data, and those for which 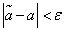 compatible with them.
compatible with them.
Let us turn to the question of finding confidential boundaries. 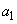 and
and 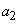 .
.
Let for parameter 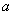 there is an unbiased estimate
there is an unbiased estimate 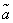 . If we knew the distribution law
. If we knew the distribution law 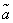 , the task of finding a confidence interval would be quite simple: it would be enough to find such a value
, the task of finding a confidence interval would be quite simple: it would be enough to find such a value 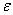 , for which
, for which
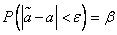 .
.
The difficulty is that the distribution law estimates 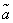 depends on the law of distribution of magnitude
depends on the law of distribution of magnitude 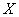 and, therefore, from its unknown parameters (in particular, from the parameter itself).
and, therefore, from its unknown parameters (in particular, from the parameter itself). 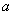 ).
).
To circumvent this difficulty, you can apply the following roughly approximate method: replace in the expression for 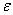 unknown parameters of their point estimates. With a relatively large number of experiments
unknown parameters of their point estimates. With a relatively large number of experiments 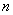 (order
(order 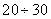 a) this method usually gives results with satisfactory accuracy.
a) this method usually gives results with satisfactory accuracy.
As an example, consider the confidence interval problem for the expectation.
Let produced 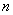 independent experiments on a random variable
independent experiments on a random variable 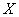 whose characteristics are mathematical expectation
whose characteristics are mathematical expectation 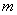 and variance
and variance 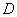 - unknown. Estimates for these parameters are obtained:
- unknown. Estimates for these parameters are obtained:
 ;
;  . (14.3.4)
. (14.3.4)
Required to build a confidence interval 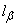 corresponding to the confidence level
corresponding to the confidence level 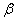 for mathematical expectation
for mathematical expectation 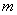 magnitudes
magnitudes 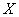 .
.
In solving this problem, we use the fact that 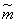 represents the sum
represents the sum 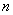 independent identically distributed random variables
independent identically distributed random variables 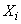 and, according to the central limit theorem, with a sufficiently large
and, according to the central limit theorem, with a sufficiently large 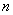 its distribution law is close to normal. In practice, even with a relatively small number of terms (about
its distribution law is close to normal. In practice, even with a relatively small number of terms (about 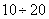 a) the distribution law of the sum can be approximately considered normal. We will proceed from the fact that
a) the distribution law of the sum can be approximately considered normal. We will proceed from the fact that 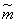 distributed according to normal law. The characteristics of this law — expectation and variance — are equal, respectively.
distributed according to normal law. The characteristics of this law — expectation and variance — are equal, respectively. 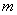 and
and 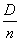 (see ch. 13
(see ch. 13 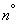 13.3). Suppose the value
13.3). Suppose the value 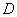 we know and find the value
we know and find the value 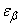 for which
for which
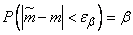 . (14.3.5)
. (14.3.5)
Applying the formula (6.3.5) of Chapter 6, we express the probability on the left side (14.3.5) through the normal distribution function
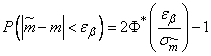 . (14.3.6)
. (14.3.6)
Where 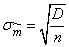 - standard deviation of assessment
- standard deviation of assessment 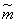 .
.
From the equation
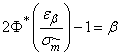
find the value 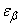 :
:
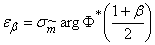 , (14.3.7)
, (14.3.7)
Where  - inverse function
- inverse function 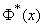 , i.e., the value of the argument for which the normal distribution function is
, i.e., the value of the argument for which the normal distribution function is 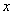 .
.
Dispersion 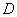 through which the value is expressed
through which the value is expressed 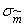 , we are not exactly known; as its approximate value, you can use the estimate
, we are not exactly known; as its approximate value, you can use the estimate 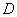 (14.3.4) and put approximately:
(14.3.4) and put approximately:
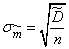 . (14.3.8)
. (14.3.8)
Thus, the problem of constructing a confidence interval, which is equal to:
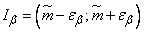 , (14.3.9)
, (14.3.9)
Where 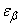 determined by the formula (14.3.7).
determined by the formula (14.3.7).
To avoid when calculating 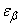 inverse interpolation in function tables
inverse interpolation in function tables 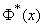 , it is convenient to make a special table (see table. 14.3.1), where the values of
, it is convenient to make a special table (see table. 14.3.1), where the values of
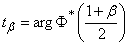
depending on the 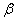 . Magnitude
. Magnitude 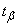 determines for the normal law the number of standard quadratic deviations that need to be postponed to the right and left of the center of dispersion in order that the probability of getting into the resulting section is equal to
determines for the normal law the number of standard quadratic deviations that need to be postponed to the right and left of the center of dispersion in order that the probability of getting into the resulting section is equal to 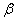 .
.
Through value 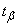 confidence interval is expressed as:
confidence interval is expressed as:
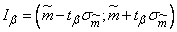 .
.
Table 14.3.1
|
|
|
|
|
|
|
|
0.80 | 1.282 | 0.86 | 1,475 | 0.91 | 1.694 | 0.97 | 2,169 |
0.81 | 1,310 | 0.87 | 1.513 | 0.92 | 1,750 | 0.98 | 2,325 |
0.82 | 1,340 | 0.88 | 1.554 | 0.93 | 1.810 | 0.99 | 2.576 |
0.83 | 1,371 | 0.89 | 1,597 | 0.94 | 1,880 | 0.9973 | 3,000 |
0.84 | 1,404 | 0.90 | 1,643 | 0.95 | 1,960 | 0.999 | 3.290 |
0.85 | 1,439 | 0.96 | 2,053 |
Example 1. Produced 20 experiments on the value 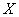 ; the results are shown in table 14.3.2.
; the results are shown in table 14.3.2.
Table 14.3.2
|
|
|
|
|
|
|
|
one | 10.5 | 6 | 10.6 | eleven | 10.6 | sixteen | 10.9 |
2 | 10.8 | 7 | 10.9 | 12 | 11.3 | 17 | 10.8 |
3 | 11.2 | eight | 11.0 | 13 | 10.5 | 18 | 10.7 |
four | 10.9 | 9 | 10.3 | 14 | 10.7 | nineteen | 10.9 |
five | 10.4 | ten | 10.8 | 15 | 10.8 | 20 | 11.0 |
Required to find a rating 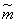 for mathematical expectation
for mathematical expectation 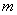 magnitudes
magnitudes 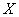 and build a confidence interval corresponding to the confidence probability
and build a confidence interval corresponding to the confidence probability 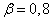 .
.
Decision. We have:
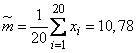 .
.
Choosing a starting point 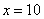 , using the third formula (14.2.14) we find the unbiased estimate
, using the third formula (14.2.14) we find the unbiased estimate 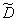 :
:
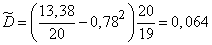 ;
;
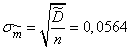 .
.
According to table 14.3.1 we find 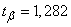 ;
;
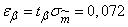 .
.
Confidence limits:
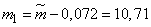 ;
;
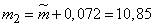 .
.
Confidence interval:
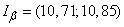 .
.
Parameter values 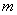 lying in this interval are consistent with the experimental data given in table 14.3.2.
lying in this interval are consistent with the experimental data given in table 14.3.2.
In a similar way, a confidence interval can also be constructed for dispersion.
Let produced 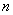 independent experiments on a random variable
independent experiments on a random variable 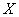 with unknown parameters
with unknown parameters 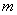 and
and 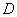 and for dispersion
and for dispersion 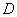 unbiased estimate received:
unbiased estimate received:
 , (14.3.11)
, (14.3.11)
Where
 .
.
It is required to approximately build a confidence interval for the variance.
From the formula (14.3.11) it can be seen that 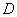 represents the sum
represents the sum 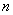 random variables of the form
random variables of the form 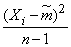 . These values are not independent, since any of them includes the value
. These values are not independent, since any of them includes the value 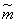 depending on everyone else. However, it can be shown that by increasing
depending on everyone else. However, it can be shown that by increasing 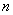 the distribution law of their sum also approaches normal. Practically at
the distribution law of their sum also approaches normal. Practically at 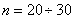 it can already be considered normal.
it can already be considered normal.
Suppose that this is so, and we find the characteristics of this law: expectation and variance. Since the evaluation 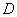 - unbiased, then
- unbiased, then
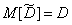 .
.
Variance calculation  associated with relatively complex calculations, so we give its expression without output:
associated with relatively complex calculations, so we give its expression without output:
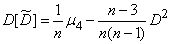 , (14.3.12)
, (14.3.12)
Where 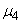 - the fourth central moment of magnitude
- the fourth central moment of magnitude 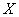 .
.
To use this expression, you need to substitute the values in it 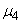 and
and 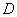 (at least approximate). Instead
(at least approximate). Instead 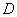 you can use his assessment
you can use his assessment 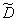 . In principle, the fourth central point
. In principle, the fourth central point 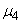 You can also replace it with an estimate, for example, a value of the form:
You can also replace it with an estimate, for example, a value of the form:
 (14.3.13)
(14.3.13)
but such a replacement will give extremely low accuracy, since in general, with a limited number of experiments, moments of high order will be determined with large errors. However, in practice it often happens that the type of distribution law 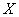 known in advance: only its parameters are unknown. Then you can try to express
known in advance: only its parameters are unknown. Then you can try to express 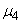 through
through 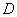 .
.
Take the most frequent case when 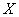 distributed according to normal law. Then its fourth central moment is expressed in terms of variance (see Ch. 6
distributed according to normal law. Then its fourth central moment is expressed in terms of variance (see Ch. 6 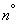 6.2):
6.2):
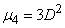 ,
,
and the formula (14.3.12) gives
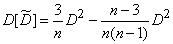
or
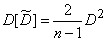 . (14.3.14)
. (14.3.14)
Replacing in (14.3.14) the unknown 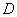 his assessment
his assessment 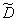 , we get:
, we get:
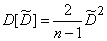 (14.3.15)
(14.3.15)
from where
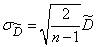 . (14.3.16)
. (14.3.16)
Moment 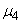 can be expressed through
can be expressed through 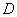 also in some other cases where the distribution of the magnitude
also in some other cases where the distribution of the magnitude 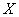 It is not normal, but its appearance is known. For example, for the law of uniform density (see Chapter 5) we have:
It is not normal, but its appearance is known. For example, for the law of uniform density (see Chapter 5) we have:
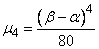 ;
;  ,
,
Where 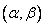 - the interval at which the law is given. Consequently,
- the interval at which the law is given. Consequently,
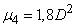 .
.
According to the formula (14.3.12) we get:
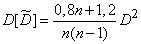 ,
,
where we find approximately
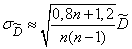 . (14.3.17)
. (14.3.17)
In cases where the type of distribution law 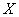 unknown, with estimated value
unknown, with estimated value 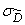 it is recommended to use the formula (14.3.16), if there are no special grounds for believing that this law is very different from normal (it has a noticeable positive or negative kurtosis).
it is recommended to use the formula (14.3.16), if there are no special grounds for believing that this law is very different from normal (it has a noticeable positive or negative kurtosis).
If approximate value 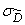 obtained in one way or another, it is possible to build a confidence interval for the variance, in the same way as we built it for the expectation:
obtained in one way or another, it is possible to build a confidence interval for the variance, in the same way as we built it for the expectation:
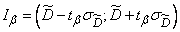 , (14.3.18)
, (14.3.18)
where is the value 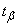 depending on a given probability
depending on a given probability 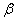 is in table 14.3.1.
is in table 14.3.1.
Example 2. Find approximately 80% confidence interval for the variance of a random variable 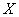 in the conditions of example 1, if it is known that
in the conditions of example 1, if it is known that 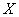 distributed according to a law close to normal.
distributed according to a law close to normal.
Decision. The value remains the same as in example 1:
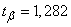 .
.
According to the formula (14.3.16)
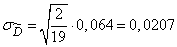 .
.
According to the formula (14.3.18) we find the confidence interval:
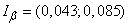 .
.
The corresponding interval of values of the standard deviation: 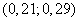 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis