Lecture
In Hamiltonian mechanics, canonical transformation (also contact transformation ) is a transformation of canonical variables and a Hamiltonian that does not change the general form of the Hamilton equations for any Hamiltonian system. Canonical transformations can also be introduced in the quantum case as non-changing form of Heisenberg equations. They allow us to reduce a problem with a certain Hamiltonian to a problem with a simpler Hamiltonian in both the classical and quantum cases. Canonical transformations form a group.
Transformations
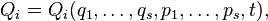
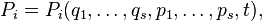
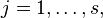 where
where  - the number of degrees of freedom
- the number of degrees of freedom
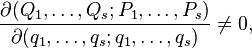
are called canonical if this transformation translates the Hamilton equations with the Hamilton function 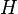 :
:
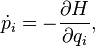
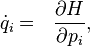
Hamilton equations with Hamilton function 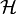 :
:
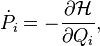

Variables 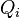 and
and 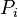 are called new coordinates and momenta, respectively, and
are called new coordinates and momenta, respectively, and 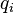 and
and 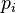 - old coordinates and pulses.
- old coordinates and pulses.
From the invariance of the Poincaré – Cartan integral and the Lee Hua-jung theorem on its uniqueness, we can obtain:
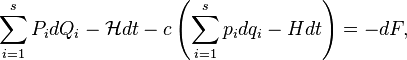
where is the constant 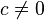 called the valence of the canonical transformation,
called the valence of the canonical transformation, 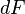 - total differential of some function
- total differential of some function 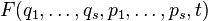 (it is assumed that
(it is assumed that 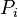 and
and 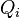 also expressed in terms of old variables). It is called the generating function of the canonical transformation. Canonical transformations are one-to-one defined by the generating function and valence.
also expressed in terms of old variables). It is called the generating function of the canonical transformation. Canonical transformations are one-to-one defined by the generating function and valence.
Canonical transformations for which 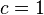 called univalent . Since for a given generating function different
called univalent . Since for a given generating function different  if the expressions for the new coordinates are changed through the old ones, and also for the Hamiltonian only by a constant, then only univalent canonical transformations are often considered.
if the expressions for the new coordinates are changed through the old ones, and also for the Hamiltonian only by a constant, then only univalent canonical transformations are often considered.
The generating function can often be expressed not through old coordinates and impulses, but through any two of the four variables. 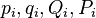 , and the choice is independent for each
, and the choice is independent for each 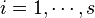 . It is convenient to express it so that for everyone
. It is convenient to express it so that for everyone 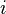 one variable was new and the other was old. There is a lemma stating that this can always be done. Differential function
one variable was new and the other was old. There is a lemma stating that this can always be done. Differential function 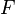 has the explicit form of the total differential in the case when it is expressed through the old and new coordinates
has the explicit form of the total differential in the case when it is expressed through the old and new coordinates 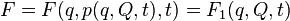 . When using other coordinate pairs, it is convenient to go to functions whose differential will have the explicit form of the total differential for the corresponding variables. For this you need to do the Legendre transform of the original function
. When using other coordinate pairs, it is convenient to go to functions whose differential will have the explicit form of the total differential for the corresponding variables. For this you need to do the Legendre transform of the original function 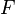 . The resulting functions are called the generating functions of the canonical transformation in the corresponding coordinates. In the case when the choice of coordinates is the same for all
. The resulting functions are called the generating functions of the canonical transformation in the corresponding coordinates. In the case when the choice of coordinates is the same for all  There are four possible choices of variables, the corresponding functions are usually denoted by numbers:
There are four possible choices of variables, the corresponding functions are usually denoted by numbers:
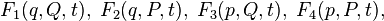
where for simplicity vectors of old velocities and impulses are introduced 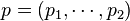 ,
, 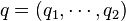 , similarly for new speeds and impulses. Such generating functions are referred to as generating functions of the 1st, 2nd, 3rd, or 4th type, respectively.
, similarly for new speeds and impulses. Such generating functions are referred to as generating functions of the 1st, 2nd, 3rd, or 4th type, respectively.
Let be 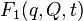 - arbitrary non-degenerate function of old coordinates, new coordinates and time:
- arbitrary non-degenerate function of old coordinates, new coordinates and time:
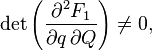
besides, some number is given 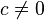 then a couple
then a couple 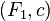 defines a canonical transformation by rule
defines a canonical transformation by rule
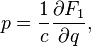
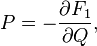
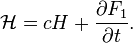
Relation to the original generating function:
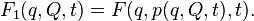
The canonical transformation can be obtained with the help of such a function if the Jacobian is not equal to zero:
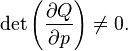
Canonical transformations supplemented with this condition are called free .
Let be 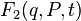 - arbitrary non-degenerate function of old coordinates, new coordinates and time:
- arbitrary non-degenerate function of old coordinates, new coordinates and time:
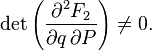
besides, some number is given 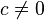 then a couple
then a couple 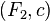 defines a canonical transformation by rule
defines a canonical transformation by rule
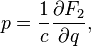
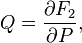
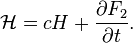
Relation to the original generating function:
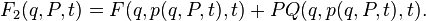
The canonical transformation can be obtained with the help of such a function if the Jacobian is not equal to zero:

Let be 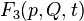 - arbitrary non-degenerate function of old coordinates, new coordinates and time:
- arbitrary non-degenerate function of old coordinates, new coordinates and time:
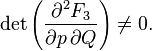
besides, some number is given 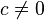 then a couple
then a couple  defines a canonical transformation by rule
defines a canonical transformation by rule
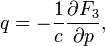
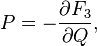
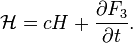
Relation to the original generating function:
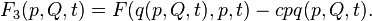
A canonical transformation can be obtained using such a function if the Jacobian is not equal to zero:
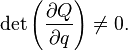
Let be 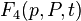 - arbitrary non-degenerate function of old coordinates, new coordinates and time:
- arbitrary non-degenerate function of old coordinates, new coordinates and time:
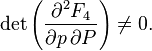
besides, some number is given 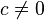 then a couple
then a couple 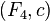 defines a canonical transformation by rule
defines a canonical transformation by rule
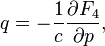
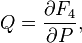
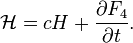
Relation to the original generating function:
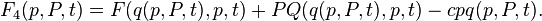
The canonical transformation can be obtained with the help of such a function if the Jacobian is not equal to zero:
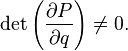
1. Identical transformation
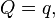
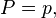
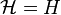
can be obtained by:

2. If you specify
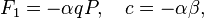
then the resulting transformation will be:
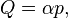
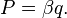
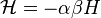
Thus, the separation of canonical variables into coordinates and impulses from a mathematical point of view is conditional.
3. Inversion conversion
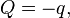
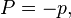
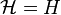
can be obtained by:
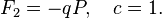
4. Point transformations (transformations in which new coordinates are expressed only through old coordinates and time, but not old impulses.)
They can always be specified using:
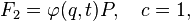
then
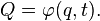
In particular, if
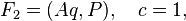
Where 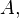 - orthogonal matrix:
- orthogonal matrix:
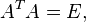
that
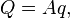
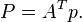
The function also leads to point transformations:
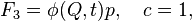
then
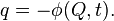
In particular, the function
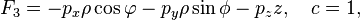
sets the transition from Cartesian to cylindrical coordinates.
5. Linear variable transformations 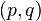 systems with one degree of freedom:
systems with one degree of freedom:
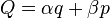

is a univalent canonical transformation with
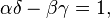
generating function:
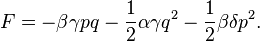
Such transformations form a special linear group. 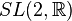 .
.
Action expressed as a function of endpoint coordinates and momenta
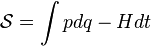
specifies the canonical transformation of the Hamiltonian system.
The necessary and sufficient condition for the canonicity of transformations can be written using the Poisson brackets:
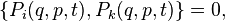
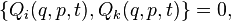
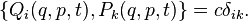
In addition, a necessary and sufficient condition for the canonicity of the transformation is the performance for arbitrary functions 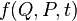 and
and 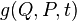 conditions:
conditions:
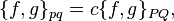
where under 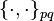 and
and 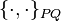 Poisson brackets are understood by the old and new coordinates, respectively.
Poisson brackets are understood by the old and new coordinates, respectively.
In the case of univalent canonical transformations:
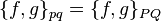
and say that Poisson brackets are invariant with respect to such transformations. Sometimes canonical transformations are defined this way (in this case, only univalent transformations are considered canonical transformations).
Similarly, the necessary and sufficient condition for the canonicity of transformations can be written using Lagrange brackets:
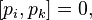
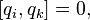
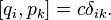
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis