Lecture
Suppose that several identical machines in the same conditions transport cargo. Any car can fail during these shipments. Let the probability of failure of one machine does not depend on the failure of other machines. This means that independent events (trials) are considered. The probability of failure of each of these machines will take the same ( 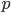 ).
).
Let, in general, be produced 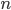 independent trials. The task is to determine the probability that exactly
independent trials. The task is to determine the probability that exactly 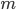 trials event will come
trials event will come 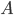 if the probability of occurrence of this event in each trial is equal
if the probability of occurrence of this event in each trial is equal 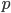 . In the case of cars, this may be the probability of failure of exactly one car, exactly two cars, etc.
. In the case of cars, this may be the probability of failure of exactly one car, exactly two cars, etc.
We first define the probability that in the first  trials event
trials event 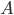 come, and in the rest
come, and in the rest  trials - will not come. The probability of such an event can be obtained on the basis of the formula for the probability of the production of independent events.
trials - will not come. The probability of such an event can be obtained on the basis of the formula for the probability of the production of independent events.
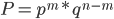 ,
,
Where 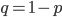 .
.
Since only one of the possible combinations was considered when an event 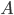 happened only in the first
happened only in the first 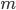 tests, then to determine the desired probability you need to go through all possible combinations. Their number will be equal to the number of combinations of
tests, then to determine the desired probability you need to go through all possible combinations. Their number will be equal to the number of combinations of 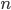 items by
items by 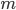 i.e.
i.e. 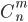 .
.
So the probability that an event 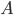 come exactly in
come exactly in 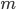 tests determined by the formula
tests determined by the formula
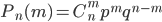 , (3.3)
, (3.3)
Where 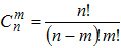 .
.
Formula (3.3) is called the Bernoulli formula.
Example. In four attempts, some items are played. The probability of winning each attempt is known and is 0.5. What is the probability of winning exactly three items?
Decision. According to the formula Bernoulli find
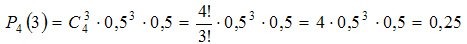
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis