Lecture
In practice, the need to linearize the function of one random argument is relatively rare: usually the cumulative effect of several random factors has to be taken into account. However, from methodological considerations it is convenient to start from this simplest case. Let there be a random variable 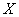 and its numerical characteristics are known: expectation
and its numerical characteristics are known: expectation 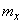 and variance
and variance 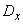 .
.
Assume that practically possible values of a random variable 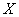 limited to
limited to 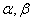 i.e.
i.e.
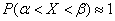 .
.
There is another random variable.  related to
related to  functional dependence:
functional dependence:
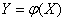 , (11.2.1)
, (11.2.1)
and function 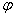 although not linear, it differs little from linear in the segment
although not linear, it differs little from linear in the segment 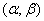 .
.
Required to find the numerical characteristics of 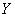 - expected value
- expected value 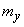 and variance
and variance 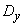 .
.
Consider the curve 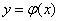 Location on
Location on 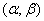 (fig. 11.2.1) and replace it with an approximately tangent at the point
(fig. 11.2.1) and replace it with an approximately tangent at the point 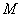 with abscissa
with abscissa 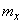 . The tangent equation is:
. The tangent equation is:
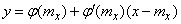 . (11.2.2)
. (11.2.2)
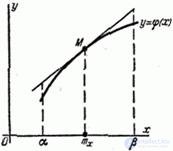
Fig. 11.2.1
Suppose that the interval of practically possible values of the argument 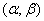 so narrow that within this interval the curve and the tangent differ little, so that the curve section can practically be replaced by the tangent section; in short, on the site
so narrow that within this interval the curve and the tangent differ little, so that the curve section can practically be replaced by the tangent section; in short, on the site 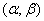 function
function 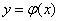 almost linear. Then random variables
almost linear. Then random variables 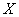 and
and 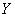 approximately related linear dependence:
approximately related linear dependence:
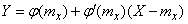 ,
,
or denoting 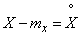 ,
,
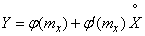 . (11.2.3)
. (11.2.3)
To the linear function (11.2.3), one can apply the well-known methods of determining the numerical characteristics of linear functions (see 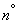 10.2). The mathematical expectation of this linear function will be found by substituting in its expression (11.2.3) the mathematical expectation of the argument
10.2). The mathematical expectation of this linear function will be found by substituting in its expression (11.2.3) the mathematical expectation of the argument 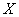 equal to zero. We get:
equal to zero. We get:
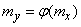 . (11.2.4)
. (11.2.4)
Variance of magnitude 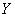 determined by the formula
determined by the formula
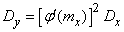 . (11.2.5)
. (11.2.5)
Turning to the standard deviation, we have:
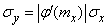 . (11.2.6)
. (11.2.6)
Formulas (11.2.4), (11.2.5), (11.2.6), of course, are approximate, since the replacement of a nonlinear function by a linear one is also approximate.
Thus, we solved the task and came to the following conclusions.
To find the expectation of an almost linear function, you need to substitute its expectation instead of an argument in the function expression. To find the variance of an almost linear function, the variance of the argument must be multiplied by the square of the derivative of the function at the point corresponding to the expectation of the argument.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis