Lecture
The distribution function of a system of two random variables 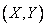 called the probability of joint fulfillment of two inequalities
called the probability of joint fulfillment of two inequalities 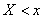 and
and 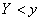 :
:
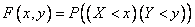 . (8.2.1)
. (8.2.1)
If we use for the geometric interpretation of the system the image of a random point, then the distribution function 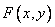 there is nothing like the probability of hitting a random point
there is nothing like the probability of hitting a random point 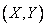 in an infinite quadrant with a vertex at a point
in an infinite quadrant with a vertex at a point  lying to the left and below it (Fig. 8.2.1). In a similar interpretation, the distribution function of one random variable
lying to the left and below it (Fig. 8.2.1). In a similar interpretation, the distribution function of one random variable 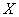 - we denote it
- we denote it 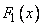 - represents the probability of hitting a random point in the half-plane, bounded to the right by the abscissa
- represents the probability of hitting a random point in the half-plane, bounded to the right by the abscissa 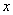 (Fig. 8.2.2); single value distribution function
(Fig. 8.2.2); single value distribution function  - probability of hitting the half-plane bounded by ordinate y (Fig. 8.2.3).
- probability of hitting the half-plane bounded by ordinate y (Fig. 8.2.3).
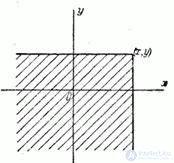
Fig. 8.2.1
AT  5.2 we gave the main properties of the distribution function
5.2 we gave the main properties of the distribution function 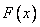 for one random variable. We formulate similar properties for the distribution function of a system of random variables and again use the geometric interpretation to illustrate these properties.
for one random variable. We formulate similar properties for the distribution function of a system of random variables and again use the geometric interpretation to illustrate these properties.
1. Distribution function 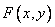 there is a non-decreasing function of both its arguments, i.e.
there is a non-decreasing function of both its arguments, i.e.
at 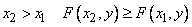 ;
;
at 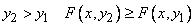 .
.
In this property of the function 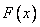 can be clearly seen using the geometric interpretation of the distribution function as the probability of falling into a quadrant with vertex
can be clearly seen using the geometric interpretation of the distribution function as the probability of falling into a quadrant with vertex  (Fig. 8.2.1). Indeed, increasing
(Fig. 8.2.1). Indeed, increasing 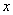 (by shifting the right edge of the quadrant to the right) or by increasing
(by shifting the right edge of the quadrant to the right) or by increasing 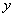 (by shifting the upper boundary upward), we obviously cannot reduce the probability of falling into this quadrant.
(by shifting the upper boundary upward), we obviously cannot reduce the probability of falling into this quadrant.
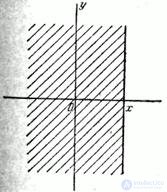

Fig. 8.2.2 Figure 8.2.3
2. Everywhere 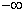 the distribution function is zero:
the distribution function is zero:
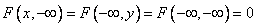 .
.
In this property we clearly see, unlimitedly pushing the right edge of the quadrant to the left 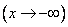 or down its upper limit
or down its upper limit 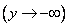 or doing it simultaneously with both boundaries; while the probability of hitting the quadrant tends to zero.
or doing it simultaneously with both boundaries; while the probability of hitting the quadrant tends to zero.
3. With one of the arguments equal to 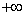 , the function of the distributed system becomes the distribution function of a random variable corresponding to another argument:
, the function of the distributed system becomes the distribution function of a random variable corresponding to another argument:
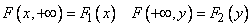 ,
,
Where 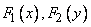 - respectively, the distribution function of the random, the distribution function of values
- respectively, the distribution function of the random, the distribution function of values 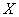 and
and 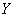 .
.
This property of the distribution function can be clearly seen by shifting one or another of the boundaries of the quadrant by 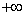 ; while in the limit the quadrant turns into a half-plane, the probability of falling into which is the distribution function of one of the quantities included in the system.
; while in the limit the quadrant turns into a half-plane, the probability of falling into which is the distribution function of one of the quantities included in the system.
4. If both arguments are equal 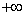 , the distribution function of the system is equal to one:
, the distribution function of the system is equal to one:
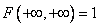 .
.
Indeed, with 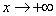 ,
, 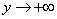 quadrant with vertex
quadrant with vertex  in the limit turns into the whole plane
in the limit turns into the whole plane  , hit in which there is a reliable event.
, hit in which there is a reliable event.
When considering the laws of distribution of individual random variables (Chapter 5), we derived an expression for the probability of a random variable falling within a given segment. We expressed this probability both through the distribution function and through the distribution density.
In a similar way for a system of two random variables is the question of the probability of hitting a random point 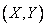 within the specified area
within the specified area 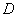 on surface
on surface  (Fig.8.2.4).
(Fig.8.2.4).
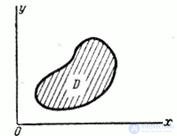
Fig. 8.2.4
Let's arrange an event consisting in hitting a random point  to the area
to the area  denote by symbol
denote by symbol 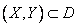 .
.
The probability of hitting a random point in a given area is expressed most simply in the case when this area is a rectangle with sides parallel to the coordinate axes.
Express through the distribution function of the system the probability of hitting a random point 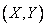 into a rectangle
into a rectangle 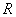 limited by abscissas
limited by abscissas 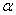 and
and 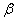 and ordinates
and ordinates 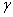 and
and  (Fig. 8.2.5).
(Fig. 8.2.5).
In this case, it should be agreed where we will refer the borders of the rectangle. In the same way as we did for one random variable, we agree to include in the rectangle 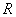 its lower and left borders and not include the upper and right. Then event
its lower and left borders and not include the upper and right. Then event 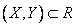 will be equivalent to the product of two events:
will be equivalent to the product of two events: 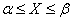 and
and 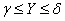 . Express the probability of this event through the distribution function of the system. To do this, look at the plane
. Express the probability of this event through the distribution function of the system. To do this, look at the plane 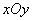 four infinite quadrants with vertices at points
four infinite quadrants with vertices at points 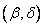 ;
; 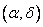 ;
; 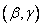 and
and 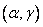 (Fig. 8.2.6).
(Fig. 8.2.6).
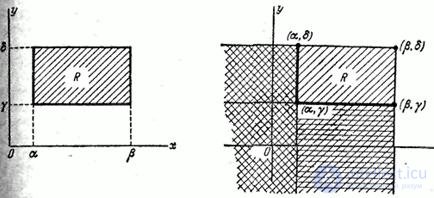
Fig. 8.2.5. Fig. 8.2.6
Obviously, the probability of hitting the rectangle 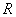 equal to the probability of falling into the quadrant
equal to the probability of falling into the quadrant 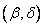 minus the probability of hitting the quadrant
minus the probability of hitting the quadrant 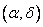 minus the probability of hitting the quadrant
minus the probability of hitting the quadrant 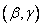 plus probability of hitting the quadrant
plus probability of hitting the quadrant 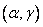 (since we twice deducted the probability of falling into this quadrant). From here we obtain a formula expressing the probability of hitting a rectangle through the distribution function of the system:
(since we twice deducted the probability of falling into this quadrant). From here we obtain a formula expressing the probability of hitting a rectangle through the distribution function of the system:
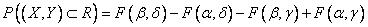 . (8.2.2)
. (8.2.2)
Later, when the notion of the distribution density of the system is introduced, we derive a formula for the probability that a random point will fall into a region of arbitrary shape.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis