Lecture
A consequence of the multiplication theorem and the full probability formula is the so-called theorem of hypotheses, or the Bayes formula.
Let's set the following task.
There is a complete group of incompatible hypotheses. 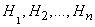 . The probabilities of these hypotheses to experience are known and equal, respectively.
. The probabilities of these hypotheses to experience are known and equal, respectively. 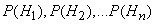 . An experiment was made, as a result of which an event was observed
. An experiment was made, as a result of which an event was observed  . The question is, how should the probabilities of hypotheses be changed due to the occurrence of this event?
. The question is, how should the probabilities of hypotheses be changed due to the occurrence of this event?
Here, essentially, it is about finding the conditional probability 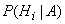 for each hypothesis.
for each hypothesis.
From the multiplication theorem we have:
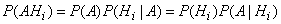
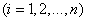 ,
,
or by discarding the left side,
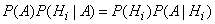
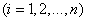 ,
,
from where
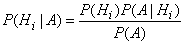
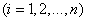 .
.
Expressing 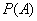 using the total probability formula (3.4.1), we have:
using the total probability formula (3.4.1), we have:
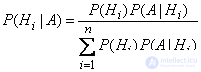
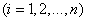 . (3.5.1)
. (3.5.1)
Formula (3.5.1) is also called the Bayes formula or hypothesis theorem.
Example 1. The device can be assembled from high-quality parts and from parts of normal quality; in general, about 40% of devices are assembled from high-quality parts. If the device is assembled from high-quality parts, its reliability (probability of failure-free operation) during 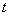 equal to 0.95; if from parts of normal quality, its reliability is 0.7. The instrument was tested over time.
equal to 0.95; if from parts of normal quality, its reliability is 0.7. The instrument was tested over time. 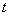 and worked flawlessly. Find the probability that it is assembled from high-quality parts.
and worked flawlessly. Find the probability that it is assembled from high-quality parts.
Decision. Two hypotheses are possible:
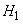 - the device is assembled from high quality parts,
- the device is assembled from high quality parts,
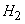 - the device is assembled from parts of normal quality.
- the device is assembled from parts of normal quality.
The probability of these hypotheses to experience:
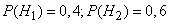 .
.
As a result of the experience, an event was observed.  - the device worked smoothly time
- the device worked smoothly time 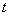 .
.
Conditional probabilities of this event under hypotheses 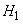 and
and 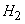 are equal:
are equal:
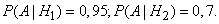
By the formula (3.5.1) we find the probability of the hypothesis 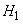 after the experience:
after the experience:
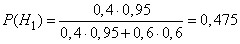 .
.
Example 2. Two shooters independently fire at one target, each making one shot. The probability of hitting the target for the first arrow is 0.8, for the second 0.4. After shooting a single hole was found in the target. Find the probability that this hole belongs to the first arrow.
Decision. Before the experiment, the following hypotheses are possible:
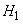 - neither the first nor the second shooter will fall,
- neither the first nor the second shooter will fall,
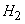 - both arrows will hit,
- both arrows will hit,
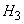 - the first shooter will fall, and the second will not,
- the first shooter will fall, and the second will not,
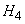 - the first shooter will not fall, and the second will.
- the first shooter will not fall, and the second will.
The probability of these hypotheses:

Conditional probabilities of the observed event  with these hypotheses are equal:
with these hypotheses are equal:
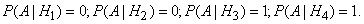
After experiencing the hypothesis 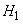 and
and 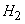 become impossible and the probabilities of hypotheses
become impossible and the probabilities of hypotheses 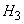 and
and 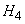 will be equal to:
will be equal to:
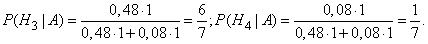
Consequently, the probability that the hole belongs to the first arrow is equal to 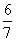 .
.
Example 3. Some object is monitored using two observation stations. The object can be in two different states. 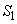 and
and 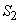 , casually going from one to another. By long-term practice it has been established that approximately 30% of the time an object is in
, casually going from one to another. By long-term practice it has been established that approximately 30% of the time an object is in 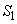 and 70% are able
and 70% are able 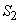 . Observation station No. 1 transmits erroneous information in approximately 2% of all cases, and observation station No. 2 in 8%. At some point, Observation Station No. 1 reported: the object is in a state
. Observation station No. 1 transmits erroneous information in approximately 2% of all cases, and observation station No. 2 in 8%. At some point, Observation Station No. 1 reported: the object is in a state 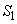 , and the observation station number 2: the object is in a state
, and the observation station number 2: the object is in a state 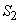 .
.
The question is: which of the messages to believe?
Decision. Naturally, to believe the message that is more likely to be true. Let's apply the Bayes formula. To do this, we make hypotheses about the state of the object:
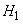 - the object is in a state
- the object is in a state 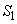 ,
,
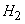 - the object is in a state
- the object is in a state 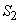 .
.
Observed event  consists of the following: station number 1 reported that the object is in a state
consists of the following: station number 1 reported that the object is in a state 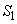 , and station number 2 - that he is in a state
, and station number 2 - that he is in a state 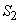 . Probabilities of hypotheses prior to experience
. Probabilities of hypotheses prior to experience
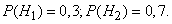
Find the conditional probabilities of the observed event.  with these hypotheses. Under hypothesis
with these hypotheses. Under hypothesis 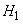 for an event to happen
for an event to happen  , you need the first station to transmit the correct message, and the second one is erroneous:
, you need the first station to transmit the correct message, and the second one is erroneous:
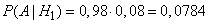 .
.
Similarly
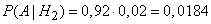 .
.
Applying the Bayes formula, we find the probability that the true state of the object is 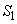 :
:
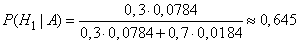 ,
,
those. of the two messages, the message of the first station is more likely.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis