Lecture
In previous chapters, we introduced methods for determining the numerical characteristics of functions of random variables; The main convenience of these methods is that they do not require finding the laws of distribution of functions. However, sometimes it becomes necessary to determine not only numerical characteristics, but also the laws of the distribution of functions.
We begin by considering the most simple problem related to this class: the problem of the distribution of the function of one random argument. Since for practice continuous random variables are most important, we will solve the problem for them.
There is a continuous random variable 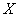 with distribution density
with distribution density 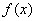 . Other random variable
. Other random variable 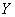 associated with her functional dependency:
associated with her functional dependency:
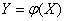 .
.
It is required to find the distribution density 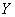 .
.
Consider the plot of the x-axis 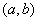 containing all possible values
containing all possible values 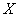 i.e.
i.e.
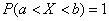 .
.
In the particular case when the range of possible values 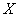 unlimited
unlimited 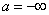 ,
, 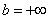 .
.
The way to solve the problem depends on the behavior of the function 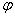 Location on
Location on 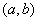 : whether it increases on this site or decreases, or fluctuates.
: whether it increases on this site or decreases, or fluctuates.
In this  we consider the case when the function
we consider the case when the function 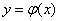 plot
plot 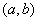 monotone. At the same time, we will analyze two cases separately: a monotone increase and a monotone decrease of a function.
monotone. At the same time, we will analyze two cases separately: a monotone increase and a monotone decrease of a function.
1. Function 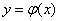 Location on
Location on 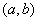 monotonously increases (fig. 12.1.1). When the magnitude
monotonously increases (fig. 12.1.1). When the magnitude 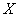 takes on different values on the plot
takes on different values on the plot 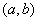 random point
random point 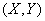 moves only along the curve
moves only along the curve 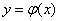 ; the ordinate of this random point is completely determined by its abscissa.
; the ordinate of this random point is completely determined by its abscissa.
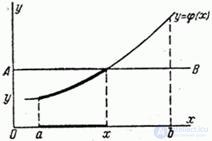
Fig. 12.1.1.
Denote 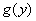 distribution density
distribution density 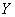 . In order to determine
. In order to determine 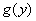 first find the distribution function of
first find the distribution function of 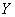 :
:
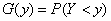 .
.
Draw a straight line 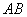 parallel to the x-axis at a distance
parallel to the x-axis at a distance 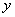 from her (Fig. 12.1.1). To satisfy the condition
from her (Fig. 12.1.1). To satisfy the condition 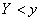 random point
random point 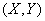 should get to that part of the curve that lies below the straight
should get to that part of the curve that lies below the straight 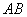 ; for this it is necessary and sufficient that the random variable
; for this it is necessary and sufficient that the random variable 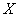 got to the plot of the x-axis from
got to the plot of the x-axis from 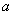 before
before 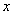 where
where 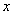 - abscissa of the intersection point of the curve
- abscissa of the intersection point of the curve 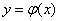 and straight
and straight 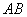 . Consequently,
. Consequently,
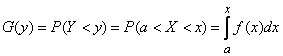 .
.
Upper limit of the integral 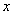 can be expressed through
can be expressed through 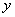 :
:
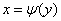 ,
,
Where 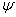 - inverse function
- inverse function 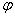 . Then
. Then
 . (12.1.1)
. (12.1.1)
Differentiating the integral (12.1.1) by variable 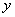 entering the upper limit, we get:
entering the upper limit, we get:
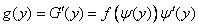 . (12.1.2)
. (12.1.2)
2. Function 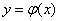 Location on
Location on 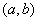 monotonously decreases (fig. 12.1.2).
monotonously decreases (fig. 12.1.2).
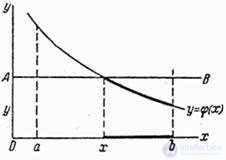
Fig. 12.1.2.
In this case
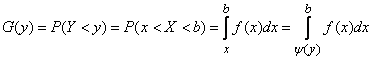 ,
,
from where
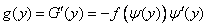 . (12.1.3)
. (12.1.3)
Comparing formulas (12.1.2) and (12.1.3), we note that they can be combined into one:
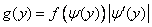 . (12.1.4)
. (12.1.4)
Indeed, when 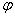 increases, its derivative (and hence
increases, its derivative (and hence 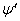 ) is positive. With decreasing function
) is positive. With decreasing function 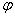 derivative
derivative 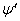 negative, but before it in the formula (12.1.3) there is a minus. Therefore, the formula (12.1.4), in which the derivative is taken in absolute value, is true in both cases. Thus, the problem of the distribution of the monotone function is solved.
negative, but before it in the formula (12.1.3) there is a minus. Therefore, the formula (12.1.4), in which the derivative is taken in absolute value, is true in both cases. Thus, the problem of the distribution of the monotone function is solved.
Example. Random value 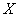 Subject to the Cauchy law with a distribution density:
Subject to the Cauchy law with a distribution density:
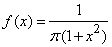 .
.
Magnitude 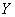 associated with
associated with 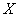 addiction
addiction
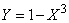 .
.
Find the density distribution 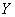 .
.
Decision. Since the function 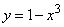 monotone on the plot
monotone on the plot 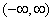 , you can apply the formula (12.1.4). We solve the problem solution in the form of two columns: in the left will be placed the notation for the functions adopted in the general solution of the problem, in the right - the specific functions corresponding to this example:
, you can apply the formula (12.1.4). We solve the problem solution in the form of two columns: in the left will be placed the notation for the functions adopted in the general solution of the problem, in the right - the specific functions corresponding to this example:
|
|
|
|
|
|
|
|
|
|
|
|
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis