Lecture
In many problems associated with normally distributed random variables, it is necessary to determine the probability of a random variable falling. 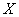 subject to normal law with parameters
subject to normal law with parameters 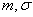 on the plot from
on the plot from 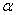 before
before 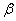 . To calculate this probability, we use the general formula
. To calculate this probability, we use the general formula
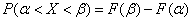 , (6.3.1)
, (6.3.1)
Where 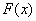 - size distribution function
- size distribution function  .
.
Find the distribution function 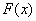 random variable
random variable 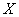 distributed according to normal law with parameters
distributed according to normal law with parameters 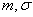 . Distribution density
. Distribution density 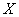 equals:
equals:
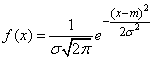 . (6.3.2)
. (6.3.2)
From here we find the distribution function
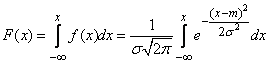 . (6.3.3)
. (6.3.3)
We make in the integral (6.3.3) a change of variable
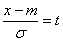
and bring it to mind:
 (6.3.4)
(6.3.4)
The integral (6.3.4) is not expressed in terms of elementary functions, but it can be calculated through a special function expressing a definite integral of the expression 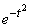 or
or 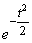 (the so-called probability integral) for which the tables are compiled. There are many types of such functions, for example:
(the so-called probability integral) for which the tables are compiled. There are many types of such functions, for example:
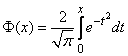 ;
; 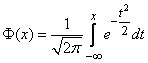
etc. Which of these functions to use is a matter of taste. We will choose as such a function
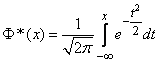 . (6.3.5)
. (6.3.5)
It is easy to see that this function is nothing but a distribution function for a normally distributed random variable with parameters 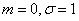 .
.
Let's call the function 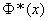 normal distribution function. The appendix (Table 1) contains tables of function values.
normal distribution function. The appendix (Table 1) contains tables of function values. 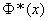 .
.
Express the distribution function (6.3.3) values 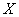 with parameters
with parameters  and
and 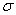 through the normal distribution function
through the normal distribution function 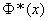 . Obviously
. Obviously
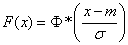 . (6.3.6)
. (6.3.6)
Now we find the probability of hitting a random variable. 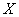 on the plot from
on the plot from 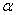 before
before 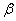 . According to the formula (6.3.1)
. According to the formula (6.3.1)
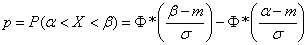 . (6.3.7)
. (6.3.7)
Thus, we have expressed the probability that a random variable will hit the section. 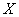 distributed according to the normal law with any parameters through the standard distribution function
distributed according to the normal law with any parameters through the standard distribution function 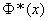 corresponding to the simplest normal law with parameters 0,1. Note that the function arguments
corresponding to the simplest normal law with parameters 0,1. Note that the function arguments 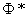 in the formula (6.3.7) have a very simple meaning:
in the formula (6.3.7) have a very simple meaning: 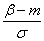 there is a distance from the right end of the plot
there is a distance from the right end of the plot 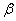 to the center of dispersion, expressed in standard deviations;
to the center of dispersion, expressed in standard deviations; 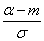 - the same distance for the left end of the section, and this distance is considered positive if the end is located to the right of the center of dispersion, and negative if it is to the left.
- the same distance for the left end of the section, and this distance is considered positive if the end is located to the right of the center of dispersion, and negative if it is to the left.
Like any distribution function, the function 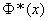 has properties:
has properties:
one. 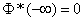 .
.
2 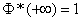 .
.
3 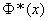 - non-decreasing function.
- non-decreasing function.
In addition, from the symmetry of the normal distribution with parameters 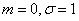 relative to the origin it follows that
relative to the origin it follows that
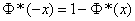 . (6.3.8)
. (6.3.8)
Using this property, strictly speaking, it would be possible to limit the function tables 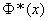 only positive values of the argument, but to avoid unnecessary operation (subtraction from one), the values in table 1 of the annex are given
only positive values of the argument, but to avoid unnecessary operation (subtraction from one), the values in table 1 of the annex are given 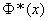 for both positive and negative arguments.
for both positive and negative arguments.
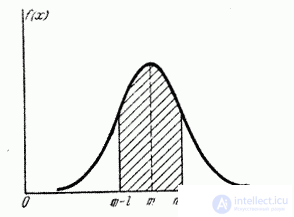
Fig. 6.3.1.
In practice, the problem of calculating the probability of a normally distributed random variable in a region symmetrical about the center of dispersion is often encountered. 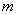 . Consider this length
. Consider this length 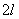 (fig. 6.3.1). We calculate the probability of hitting this area by the formula (6.3.7):
(fig. 6.3.1). We calculate the probability of hitting this area by the formula (6.3.7):
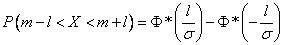 . (6.3.9)
. (6.3.9)
Given the property (6.3.8) of the function 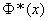 and giving the left side of the formula (6.3.9) a more compact form, we obtain the formula for the probability of a random variable falling on the area symmetric about the center of dispersion according to the normal law:
and giving the left side of the formula (6.3.9) a more compact form, we obtain the formula for the probability of a random variable falling on the area symmetric about the center of dispersion according to the normal law:
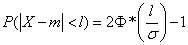 . (6.3.10)
. (6.3.10)
We solve the following problem. Set aside from the center of dispersion 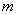 consecutive lengths
consecutive lengths 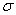 (Fig. 6.3.2) and calculate the probability of hitting a random variable
(Fig. 6.3.2) and calculate the probability of hitting a random variable 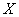 in each of them. Since the curve of the normal law is symmetric, it is enough to postpone such segments only in one direction.
in each of them. Since the curve of the normal law is symmetric, it is enough to postpone such segments only in one direction.
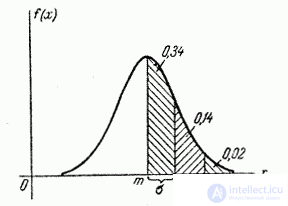
Fig. 6.3.2.
By the formula (6.3.7) we find:
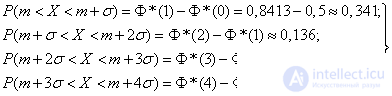 (6.3.11)
(6.3.11)
As can be seen from these data, the probabilities of hitting each of the following segments (fifth, sixth, etc.) with an accuracy of up to 0.001 are equal to zero.
Rounding the probabilities of hitting the segments to 0.01 (up to 1%), we get three numbers that are easy to remember:
0.34; 0.14; 0.02.
The sum of these three values is 0.5. This means that for a normally distributed random variable, all the dispersions (up to fractions of a percent) fit into the area 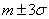 .
.
This allows, knowing the mean square deviation and the mathematical expectation of a random variable, to roughly indicate the interval of its practically possible values. This method of estimating the range of possible values of a random variable is known in mathematical statistics as the “three sigma rule”. The approximate method of determining the standard deviation of a random variable also follows from the rule of three sigma: take the maximum practically possible deviation from the average and divide it into three. Of course, this rude reception can be recommended only if there are no other, more accurate ways to determine 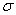 .
.
Example 1. Random variable 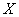 , distributed according to the normal law, is a measurement error of a certain distance. When measuring a systematic error in the direction of overestimation of 1.2 (m); the standard deviation of the measurement error is 0.8 (m). Find the probability that the deviation of the measured value from the true value does not exceed the absolute value of 1.6 (m).
, distributed according to the normal law, is a measurement error of a certain distance. When measuring a systematic error in the direction of overestimation of 1.2 (m); the standard deviation of the measurement error is 0.8 (m). Find the probability that the deviation of the measured value from the true value does not exceed the absolute value of 1.6 (m).
Decision. Measurement error is random 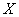 subject to normal law with parameters
subject to normal law with parameters 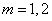 and
and 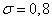 . It is necessary to find the probability of hitting this quantity from
. It is necessary to find the probability of hitting this quantity from 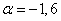 before
before 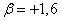 . By the formula (6.3.7) we have:
. By the formula (6.3.7) we have:
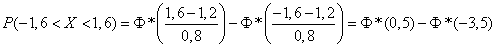 .
.
Using function tables 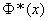 (Appendix, Table 1), we find:
(Appendix, Table 1), we find:
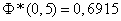 ;
; 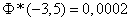 ,
,
from where
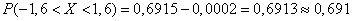 .
.
Example 2. Find the same probability as in the previous example, but under the condition that there is no systematic error.
Decision. According to the formula (6.3.10), assuming 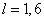 , we will find:
, we will find:
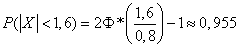 .
.
Example 3. The target, having the form of a strip (freeway), whose width is equal to 20 m, is fired in the direction perpendicular to the freeway. Aiming is on the middle line of the highway. The standard deviation in the direction of shooting is 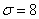 m. There is a systematic error in the direction of shooting: 3 m undershoot. Find the probability of hitting the freeway with one shot.
m. There is a systematic error in the direction of shooting: 3 m undershoot. Find the probability of hitting the freeway with one shot.
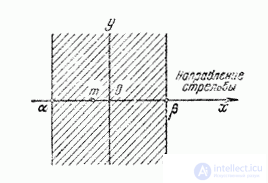
Fig. 6.3.3.
Decision. Select the origin at any point on the middle line of the motorway (Fig. 6.3.3) and direct the x-axis perpendicular to the motorway. Hitting or missing a projectile on a freeway is determined by the value of only one coordinate of the drop point 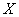 (other coordinate
(other coordinate 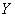 we are indifferent). Random value
we are indifferent). Random value  distributed according to normal law with parameters
distributed according to normal law with parameters 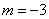 ,
, 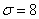 . The projectile hit the freeway corresponds to the hit value
. The projectile hit the freeway corresponds to the hit value 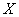 on the plot from
on the plot from 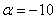 before
before 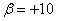 . Applying the formula (6.3.7), we have:
. Applying the formula (6.3.7), we have:
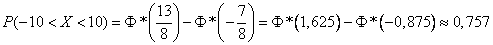 .
.
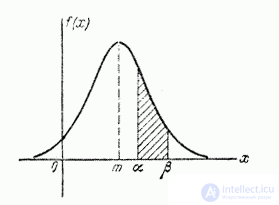
Fig. 6.3.4.
Example 4. There is a random variable 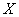 , normally distributed, with a dispersion center
, normally distributed, with a dispersion center 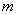 (fig. 6.3.4) and some section
(fig. 6.3.4) and some section 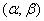 abscissa axis. What should be the standard deviation
abscissa axis. What should be the standard deviation 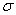 random variable
random variable 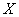 in order to probability of hitting
in order to probability of hitting 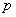 on the plot
on the plot 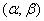 reached the maximum?
reached the maximum?
Decision. We have:
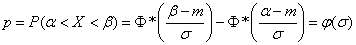 .
.
Let's differentiate this function 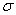 :
:
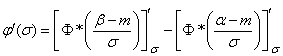 ,
,
but
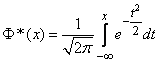 .
.
Applying the rule of differentiation of an integral with respect to a variable entering its limit, we obtain:
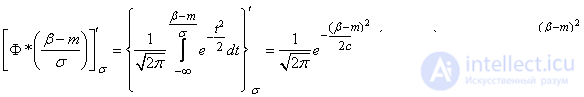 .
.
Similarly
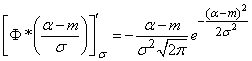 .
.
To find the extremum, we set:
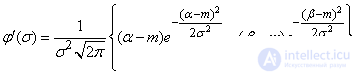 . (6.3.12)
. (6.3.12)
With 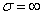 this expression vanishes and the probability
this expression vanishes and the probability 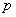 reaches a minimum. Maximum
reaches a minimum. Maximum  get from the condition
get from the condition
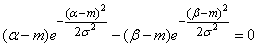 . (6.3.13)
. (6.3.13)
Equation (6.3.13) can be solved numerically or graphically.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis