Lecture
Let in the coordinate system 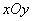 Two independent random vectors are given:
Two independent random vectors are given: 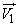 with components
with components 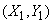 and
and 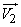 with component
with component 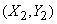 . Suppose that each of them is distributed normally, and the parameters of the first vector are equal
. Suppose that each of them is distributed normally, and the parameters of the first vector are equal
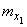 ,
, 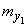 ,
, 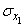 ,
, 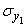 ,
, 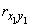 ,
,
and the parameters of the second are
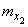 ,
, 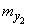 ,
, 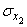 ,
, 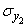 ,
, 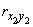 .
.
It is required to determine the distribution law of a random vector. 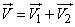 (fig. 12.8.1), whose components are equal to:
(fig. 12.8.1), whose components are equal to:
 ;
;
 .
.
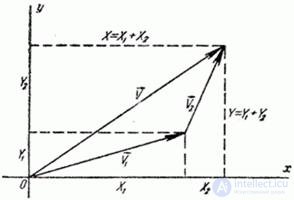
Fig. 12.8.1.
It is not difficult to prove qualitatively (in the same way as we did for the case of the composition of two normal laws in  12.6) that the vector
12.6) that the vector  also distributed normally. We will accept this provision without special proof.
also distributed normally. We will accept this provision without special proof.
Define the parameters of the law of distribution of the vector 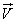 .
.
By the theorem of addition of mathematical expectations
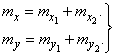 (12.8.1)
(12.8.1)
According to the theorem of addition of variances
 (12.8.2)
(12.8.2)
By the addition theorem of correlation moments
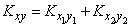 ,
,
or, going to the correlation coefficients,
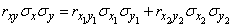 ,
,
from where
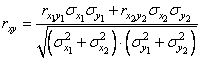 . (12.8.3)
. (12.8.3)
Thus, the problem of composition of normal laws on a plane is solved by formulas (12.8.1), (12.8.2) and (12.8.3).
These formulas are derived for the case when both the original normal laws (for vectors 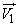 and
and 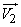 ) are set in the same coordinate system
) are set in the same coordinate system 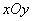 . In practice, sometimes there is a case when it is necessary to produce a composition of two normal laws on a plane, each of which is specified in its own coordinate system, namely in its main scattering axes. We give the method of composition of normal laws for this case.
. In practice, sometimes there is a case when it is necessary to produce a composition of two normal laws on a plane, each of which is specified in its own coordinate system, namely in its main scattering axes. We give the method of composition of normal laws for this case.
Let on the plane  (fig. 12.8.2) are given two normally distributed uncorrelated random vectors
(fig. 12.8.2) are given two normally distributed uncorrelated random vectors  and
and  .
.
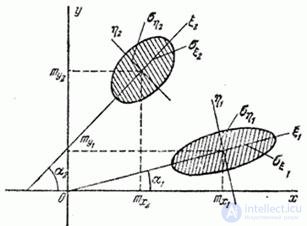
Fig. 12.8.2.
Each of the vectors is characterized by its single scattering ellipse: vector 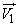 - an ellipse with the center at the point
- an ellipse with the center at the point 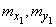 with semiaxes
with semiaxes 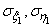 of which the first forms with the axis
of which the first forms with the axis 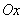 angle
angle 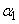 ; similar characteristics for the vector
; similar characteristics for the vector 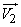 will be:
will be: 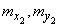 ,
, 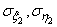 ,
, 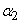 . It is required to find the parameters of a single scattering ellipse characterizing a vector
. It is required to find the parameters of a single scattering ellipse characterizing a vector 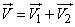 . Denote them
. Denote them
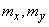 ,
, 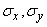 ,
, 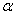 .
.
Since the position of the center of dispersion does not depend on the choice of the coordinate system, obviously, the following relations will be valid:
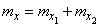 ,
,
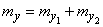 .
.
In order to find the elements of the correlation matrix of the vector 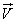 , we project random points corresponding to vectors
, we project random points corresponding to vectors 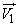 and
and 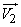 on the axis
on the axis 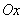 and
and  . Using the formula (10.3.3), we get:
. Using the formula (10.3.3), we get:
 (12.8.4)
(12.8.4)
Correlation coefficients of component vectors 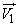 and
and 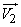 in coordinate system
in coordinate system 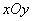 we find from the relation (9.2.2):
we find from the relation (9.2.2):
 (12.8.5)
(12.8.5)
Further, the task of composing normal laws on the plane is reduced to the previous one. Knowing 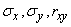 , you can find the angles compiled by the axes of the total ellipse with the abscissa axis, according to the formula (9.2.2):
, you can find the angles compiled by the axes of the total ellipse with the abscissa axis, according to the formula (9.2.2):
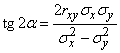 , (12.8.6)
, (12.8.6)
and main standard deviations - according to the formulas (9.2.4):
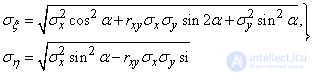 (12.8.7)
(12.8.7)
The last ratios are valid not only for standard deviations, but also for proportional probable deviations:
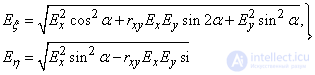 (12.8.8)
(12.8.8)
Let us turn to the composition of an arbitrary number of normal laws on the plane.
We encounter the simplest case of the composition of an arbitrary number of formal laws when the main scattering axes for all the laws subject to composition are parallel to each other. Then, choosing coordinate axes parallel to these main axes of dispersion, we will deal with systems of independent random variables, and the composition of normal laws is carried out using simple formulas:
 (12.8.9)
(12.8.9)
Where 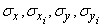 - main standard deviations of the relevant laws.
- main standard deviations of the relevant laws.
In the case when the directions of the main axes do not coincide, you can compose several normal laws by the same method that we used above for the two laws, that is, by projecting the folding random vectors on the axis of the same coordinate system.
In practice, there are often cases when, among the laws subject to composition, there are so-called “degenerate” laws, that is, laws characterized by an ellipse of dispersion that have only one semi-axis (the other is zero). Such "degenerate" laws give dispersion only in one direction. When composing such laws, one should do the same as when composing ordinary laws, setting some parameters (standard quadratic or probable deviations) equal to zero.
Example 1. The bombing error is caused by the combined effect of the following factors:
1) technical dispersal of bombs;
2) inaccuracy of aiming in range;
3) inaccurate aiming in the lateral direction.
All of these factors are independent. Technical dispersal of bombs gives a single ellipse of dispersion in the form of a circle with a radius of 20 m. The aiming error in range acts only in the direction of flight and has a standard deviation of 40 m; the center of dispersion is shifted forward in flight by 5 m. The error in lateral pickup acts only in the direction perpendicular to the flight, and has a standard deviation of 30 m; the center of dispersion is shifted to the right by 10 m. Find the parameters of the normal law, which is subject to the total error of bombing, caused by the combined action of all these factors.
Decision. Since the main axes of all the ellipses listed in the problem (of which the second and third are degenerate) are parallel, we can apply the rule of composition of normal laws with independent components (formulas (12.8.9)). Choosing axis  in the direction of flight, axis
in the direction of flight, axis  - perpendicular to it, we have:
- perpendicular to it, we have:
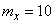 ,
, 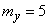 ,
,
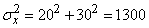 ,
, 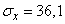 (m)
(m)
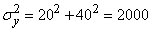 ,
, 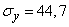 (m)
(m)
Example 2. Airborne firing from an airplane at an airplane; The scattering of hit points is considered on a vertical plane perpendicular to the direction of fire. The reasons for the scattering of the hit points are as follows:
1) errors associated with the heterogeneity of the ballistics of the shells and the fluctuations of the installation;
2) aiming errors;
3) errors caused by inaccurate determination of the range;
4) instrumental errors of sight.
The main axes of dispersion caused by the first cause are horizontally and vertically arranged, and the main root-mean-square deviations are equal to 1 and 2 m, respectively; error pickup gives a circular dispersion with an average square deviation of 3 m; the error caused by the inaccuracy of the determination of the distance, gives scattering only along an axis inclined to the horizon at an angle of 30 °, with sc. 4 m; instrumental errors of sight give circular dispersion with sko. 2 m. Systematic errors are zero.
It is required to find the parameters of the distribution law of the total error caused by all the factors listed.
Decision. Choose a coordinate system with a horizontal axis  and vertical
and vertical  . These axes are the main axes of dispersion for all laws except the third (errors due to inaccuracy in determining the distance). Denote the components of each error in the coordinate system
. These axes are the main axes of dispersion for all laws except the third (errors due to inaccuracy in determining the distance). Denote the components of each error in the coordinate system  respectively:
respectively:
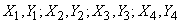 .
.
The parameters of these components are equal respectively:
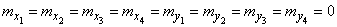 ;
;
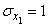 ;
; 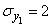 ;
; 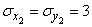 ;
; 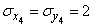 .
.
As for quantities 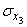 and
and 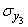 , we define them by projecting a random point
, we define them by projecting a random point 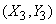 on axis
on axis 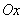 and
and  according to the formulas (12.8.4):
according to the formulas (12.8.4):
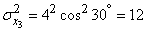 ;
;
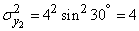 .
.
Coefficient of correlation values 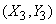 find by the formula (12.8.5)
find by the formula (12.8.5)
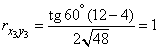 ,
,
which is natural, since the dispersion is concentrated on one straight line and, therefore, 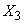 and
and 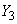 functionally dependent.
functionally dependent.
Using the theorem of addition of dispersions, we have:
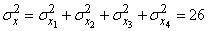 ;
; 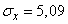 (m);
(m);
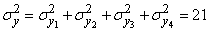 ;
; 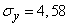 (m)
(m)
Correlation coefficient 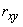 find, applying the theorem of addition of correlation moments:
find, applying the theorem of addition of correlation moments:
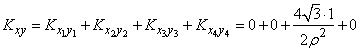 ,
,
from where
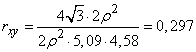 .
.
Determine the angle 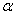 which makes up with the axis the first main axis of dispersion:
which makes up with the axis the first main axis of dispersion:
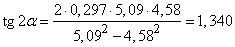 ,
,
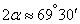 ;
; 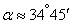 .
.
By the formulas (12.8.8) we have:
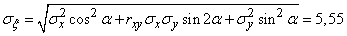 (m);
(m);
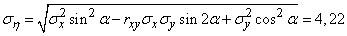 (m)
(m)
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis