Lecture
x i - values of X ,
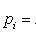
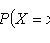
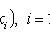
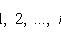
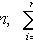
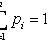

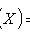
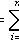
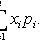
Properties:
1) M ( C ) = C , C is a constant;
2) M ( CX ) = CM ( X );
3) M ( X 1 + X 2 ) = M ( X 1 ) + M ( X 2 ), where X 1 , X 2 are independent random variables;
4) M ( X 1 X 2 ) = M ( X 1 ) M ( X 2 ).

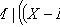
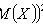
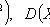
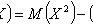
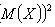
Properties:
1) D ( C ) = 0;
2) D ( CX ) = C 2 D ( X );
3) D ( X 1 + X 2 ) = D ( X 1 ) + D ( X 2 ), where X 1 , X 2 are independent random variables.
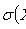
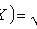
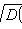
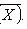
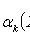
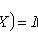
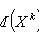
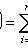
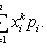
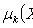
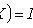
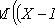
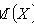
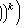
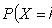
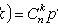
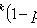

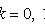
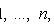
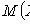
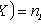
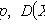
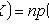
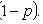
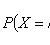
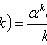
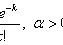
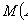
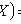
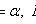
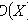
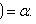
Chebyshev Inequality
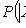
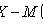
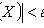


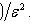
Chebyshev theorem
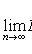
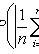
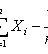
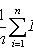
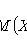
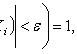
X i - pairwise independent random variables; 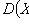
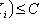 ; C is a constant.
; C is a constant.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis