Lecture
Probability density 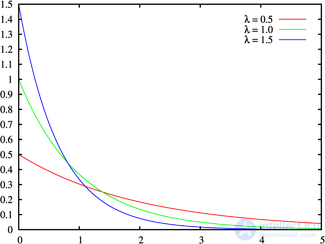 | |
Distribution function 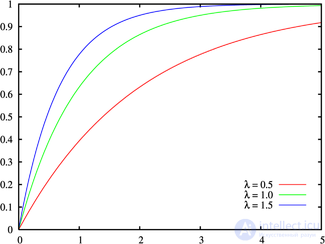 | |
| Designation | 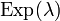 |
| Options | 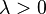 - intensity or inverse scale factor - intensity or inverse scale factor |
| Carrier | 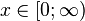 |
| Probability density | 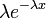 |
| Distribution function | 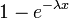 |
| Expected value | 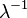 |
| Median | 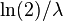 |
| Fashion | 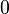 |
| Dispersion | 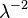 |
| Asymmetry coefficient | 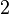 |
| Coefficient of kurtosis | 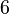 |
| Informational entropy | 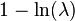 |
| Generating function of moments | 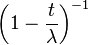 |
| Characteristic function | 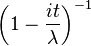 |
The exponential or exponential distribution is an absolutely continuous distribution that simulates the time between two successive accomplishments of the same event.
Random value 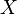 has an exponential distribution with the parameter
has an exponential distribution with the parameter 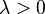 if its density is
if its density is
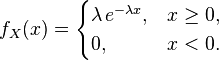 .
. Example. Suppose there is a store in which buyers enter from time to time. Under certain assumptions, the time between occurrences of two consecutive buyers will be a random variable with an exponential distribution. The average waiting time for a new customer (see below) is 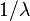 . Parameter itself
. Parameter itself 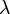 then it can be interpreted as the average number of new customers per unit of time.
then it can be interpreted as the average number of new customers per unit of time.
In this paper, for definiteness, we will assume that the density of an exponential random variable 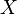 given by the first equation, and we will write:
given by the first equation, and we will write: 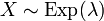 .
.
Integrating the density, we obtain the exponential distribution function:
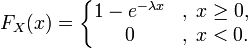
By simple integration, we find that the generating function of moments for the exponential distribution has the form:
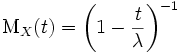 ,
, where do we get all the moments:
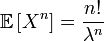 .
. In particular,
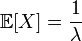 ,
, 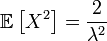 ,
, 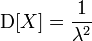 .
. Let be 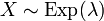 . Then
. Then 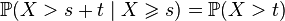 .
.
Example. Let the buses come to a stop randomly, but with some fixed average intensity. Then the amount of time already spent by the passenger on waiting for the bus does not affect the time that he still has to wait.
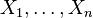 independent random variables, and
independent random variables, and 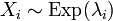 . Then
. Then 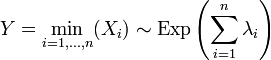 .
. 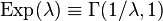 .
. 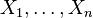 independent random variables, and
independent random variables, and 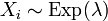 . Then
. Then 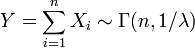 .
. 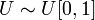 . Then
. Then 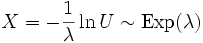 .
. 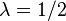 - This is a special case of the chi-square distribution:
- This is a special case of the chi-square distribution: 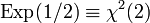
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis