Lecture
We use the general method outlined above to solve one particular problem that is practical for practice, namely, to find the distribution law for the sum of two random variables.
There is a system of two random variables. 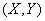 with distribution density
with distribution density 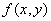 . Consider the sum of random variables.
. Consider the sum of random variables. 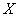 and
and 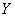 :
:
 ,
,
and find the distribution law 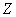 . To do this, build on the plane
. To do this, build on the plane 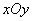 line whose equation
line whose equation 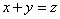 (fig. 12.5.1). This is a straight line that cuts off segments on the axes that are equal to
(fig. 12.5.1). This is a straight line that cuts off segments on the axes that are equal to 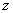 . Straight
. Straight 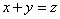 divides the plane
divides the plane 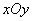 into two parts; to the right and above her
into two parts; to the right and above her 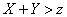 ; to the left and below
; to the left and below 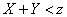 . Region
. Region 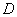 in this case, the lower left part of the plane
in this case, the lower left part of the plane 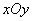 shaded in fig. 12.5.1. According to the formula (12.4.2) we have:
shaded in fig. 12.5.1. According to the formula (12.4.2) we have:
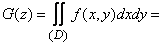
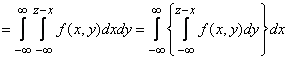 .
.
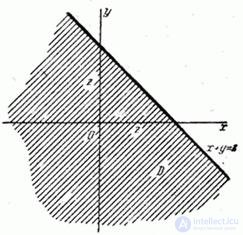
Fig. 12.5.1.
Differentiating this expression by variable 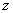 entering into the upper limit of the internal integral, we obtain:
entering into the upper limit of the internal integral, we obtain:
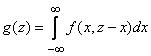 . (12.5.1)
. (12.5.1)
This is a general formula for the distribution density of the sum of two random variables.
For reasons of symmetry of the problem with respect to 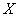 and
and 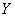 You can write another version of the same formula:
You can write another version of the same formula:
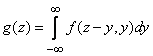 , (12.5.2)
, (12.5.2)
which is equivalent to the first and can be used instead.
Of particular practical importance is the case when the added random variables 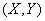 are independent. Then they talk about the composition of the laws of distribution.
are independent. Then they talk about the composition of the laws of distribution.
To make the composition of two laws of distribution it means to find the law of distribution of the sum of two independent random variables subordinate to these laws of distribution.
We derive a formula for the composition of two laws of distribution. There are two independent random variables. 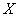 and
and 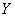 subordinate according to the laws of distribution
subordinate according to the laws of distribution 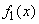 and
and 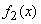 ; it is required to produce a composition of these laws, i.e., to find the density distribution of the quantity
; it is required to produce a composition of these laws, i.e., to find the density distribution of the quantity
 .
.
As magnitudes 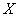 and
and 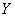 independent then
independent then
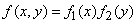 ,
,
and formulas (12.5.1) and (12.5.2) take the form:
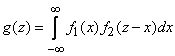 , (12.5.3)
, (12.5.3)
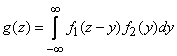 . (12.5.4)
. (12.5.4)
A symbolic notation is often used to denote the composition of the distribution laws
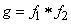 ,
,
Where 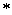 - the symbol of the composition.
- the symbol of the composition.
Formulas (12.5.3) and (12.5.4) for the composition of the laws of distribution are convenient only when the laws of distribution 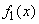 and
and 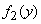 (or at least one of them) are given by one formula for the whole range of argument values (from
(or at least one of them) are given by one formula for the whole range of argument values (from 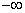 before
before 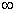 ). If both laws are set at different sites by different equations (for example, two laws of uniform density), then it is more convenient to use the general method directly, described in
). If both laws are set at different sites by different equations (for example, two laws of uniform density), then it is more convenient to use the general method directly, described in 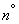 12.4, i.e. calculate the distribution function
12.4, i.e. calculate the distribution function 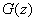 magnitudes
magnitudes  and differentiate this function.
and differentiate this function.
Example 1. Compose the composition of a normal law:
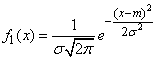
and the law of uniform density:
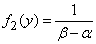 at
at 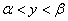 .
.
Decision. Let us apply the formula of the composition of the laws of distribution in the form (12.5.4):
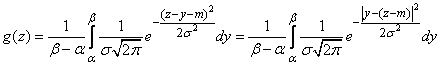 . (12.5.5)
. (12.5.5)
The integrand function in expression (12.5.5) is nothing more than a normal law with a scattering center 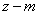 and standard deviation
and standard deviation 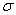 , and the integral in expression (12.5.5) is the probability that a random variable subject to this law will hit a plot from
, and the integral in expression (12.5.5) is the probability that a random variable subject to this law will hit a plot from 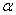 before
before 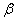 ; Consequently,
; Consequently,
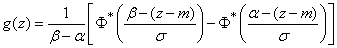 .
.
Law Charts 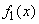 ,
, 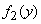 and
and 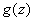 at
at 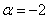 ,
, 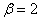 ,
, 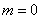 ,
, 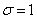 are shown in fig. 12.5.2.
are shown in fig. 12.5.2.
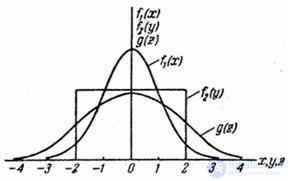
Fig. 12.5.2.
Example 2. Compose two laws of uniform density, given in the same area 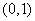 :
:
 at
at 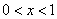 ,
,
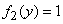 at
at  .
.
Decision. Since the laws 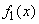 and
and 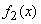 only specified on certain axes
only specified on certain axes 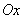 and
and 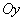 , for solving this problem, it is more convenient to use not the formulas (12.5.3) and (12.5.4), but the general method outlined in
, for solving this problem, it is more convenient to use not the formulas (12.5.3) and (12.5.4), but the general method outlined in 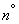 12.4, and find the distribution function
12.4, and find the distribution function 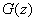 magnitudes
magnitudes  .
.
Consider a random point 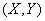 on surface
on surface 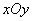 . The area of its possible positions is a square.
. The area of its possible positions is a square.  with a side equal to 1 (Fig. 12.5.3).
with a side equal to 1 (Fig. 12.5.3).
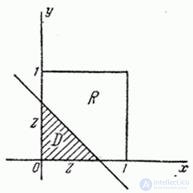
Fig. 12.5.3.
We have
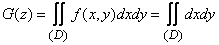 ,
,
where is the area 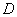 - part of the square
- part of the square 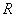 lying to the left and below the straight line
lying to the left and below the straight line 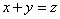 . Obviously
. Obviously
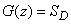 ,
,
Where 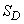 - area of the region
- area of the region 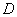 .
.
Let's make expression for the area of area 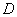 at different values
at different values 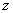 taking advantage of rice 12.5.3 and 12.5.4:
taking advantage of rice 12.5.3 and 12.5.4:
1) at 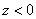
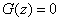 ;
;
2) at 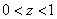
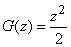 ;
;
3) at 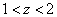
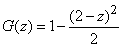 ;
;
4) at 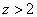
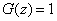 .
.
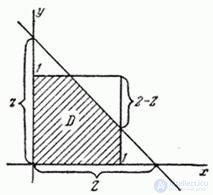
Fig. 12.5.4.
Differentiating these expressions, we get
1) at 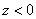
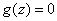 ;
;
2) at 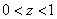
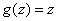 ;
;
3) at 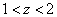
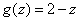 ;
;
4) at 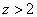
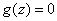 .
.
Distribution law 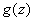 given in fig. 12.5.5. Such a law is called "Simpson's Law" or "Triangle Law".
given in fig. 12.5.5. Such a law is called "Simpson's Law" or "Triangle Law".
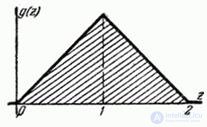
Fig. 12.5.5.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis