Quantile

Quantile in mathematical statistics is a value that a given random variable does not exceed with a fixed probability.

Definition

Consider probabilistic space 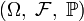and 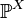- a probability measure specifying the distribution of a random variable 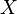. Let it be fixed 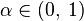. Then 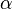quantile (or level quantile 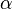a) distribution 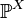called number 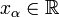such that

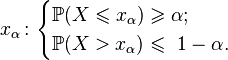
In some sources (for example, in English literature) -Oh quantile is called level quantile , i.e 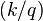-quantile in the previous notation.

Remarks

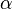• If the distribution is continuous, then -quantile is uniquely given by the equation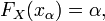

Where 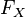- distribution function .

• Obviously, for continuous distributions, the following equality, which is widely used in the construction of confidence intervals, is true:

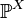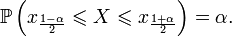
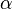• For empirical distribution -quantile can be set as follows:

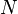1. we make a variation range of values (sample has volume ), and also consider that 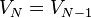(this is necessary when calculating 100% quantile using the formulas below);
2. find the value ;
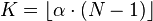3. compare and :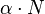

a) if 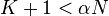then we assume ;

b) if then we assume ;

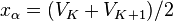c) if 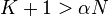then we assume .

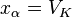Specified in this way 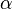-quantile satisfies the above definition.

In some cases (with a large sample size and an empirical distribution close to continuous) instead of equality you can use an approximate comparison 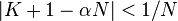(this will allow, for example, the level 1/3 quantile to be represented as 0.33 ... 333 during computer processing of data).

Median and quartile

Quantile normal distribution

• 0,25-quantile is called the first (or lower) quartile (from the Latin. Quarta - a quarter);
• 0.5-quantile is called the median (from the Latin. Mediāna - middle) or the second quartile ;
• 0,75-quantile is called the third (or upper) quartile .

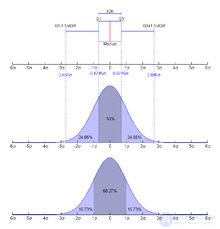
Interquartile range is the difference between the third and first quartiles, i.e. . Interquartile range is a characteristic of the spread of the distribution of magnitude and is a robust analogue of the dispersion. Together, the median and interquartile range can be used instead of the expectation and variance in the case of distributions with large outliers, or if it is impossible to calculate the latter.

Decile

A decile characterizes the distribution of aggregate values, in which nine values ​​of a decile divide it into ten equal parts. Any of these ten parts is 1/10 of the entire population. So, the first decile separates 10% of the smallest values ​​lying below the decile from 90% of the largest values ​​lying above the decile.

Just as in the case of mode and median, in the interval variational distribution series, each decile (and quartile) belongs to a certain interval and has a well-defined value ^[1] .

Percentile

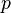th percentile is called level quantile 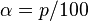. In this case, percentiles are usually considered for whole 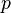, although this requirement is not mandatory ^{[ source not specified 74 days ]} . Accordingly, the median is the 50th percentile, and the first and third quartile are the 25th and 75th percentiles.

In general, the concepts of quantile and percentile are interchangeable ^{[the source is not specified 74 days ]} , as well as the scale of calculus of probabilities - absolute and percentage.

Percentiles are also called percentiles or centiles .

Quantiles of the standard normal distribution