13.6. Mass random phenomena and the central limit theorem

Previous we considered various forms of the law of large numbers. All these forms, no matter how different they are, state one thing: the fact of convergence in the probability of certain random variables to certain constants. None of the forms of the law of large numbers deals with the laws of the distribution of random variables. Limit distribution laws form the subject of another group of theorems — the central limit theorem, which is sometimes called the “quantitative form of the law of large numbers”.

All forms of the central limit theorem are devoted to establishing the conditions under which the normal distribution law arises. Since these conditions are very often fulfilled in practice, the formal law is the most common of the distribution laws most often encountered in random phenomena of nature. It occurs in all cases when the random variable under investigation can be represented as the sum of a sufficiently large number of independent (or weakly dependent) elementary terms, each of which separately has relatively little effect on the sum.

In the theory of shooting, the normal distribution law plays a particularly important role, since in most cases the practice coordinates of the hit points and projectile rupture points are distributed according to the normal law. This can be explained by the following example.

Let it be shooting at some flat target, with its center (aiming point) is the origin of coordinates. The hit point is characterized by two random variables: 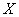and 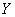. Consider one of them, for example, the deviation 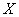point of impact from the target in the direction of the axis 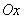. This deviation is caused by the cumulative effect of a very large number of relatively small factors, such as: aiming error, error in determining the distance to the target, vibration of the gun and the installation during shooting, errors in the manufacture of the projectile, atmospheric conditions, etc. Each of these reasons creates an elementary error - the deviation of the projectile from the target, and the coordinate of the projectile 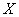can be represented as the sum of such elementary deviations:

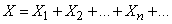, (13.6.1)

Where 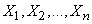- deviations caused by individual factors. Since there are a lot of these factors, they are mostly independent between themselves and, depending on the effect on the sum, individual terms can be considered approximately evenly small, the applicability conditions of the central limit theorem are obvious, and the quantity (13.6.1) should obey the distribution law close to normal .

Let us dwell in more detail on our statement about the approximately uniformly small influence of each of the terms on the sum. Its meaning is that among the elementary mistakes of shooting there is not one sharply prevailing over the sum of all the others. Indeed, if such a mistake were made, one should think that by drawing up the rules of firing or constructing an aiming device, we would try to eliminate this mistake and take into account in advance the most significant reason for the projectile deflecting from the target. Unaccounted random factors that create dispersion are usually characterized by their uniform smallness and the absence among them sharply prevailing. That is why the law of distribution of the points of impact of shells (or the law of distribution of points of rupture of shells during remote firing) is usually assumed normal.

The normal distribution law is dominant not only in the theory of firing, but also in many other areas, for example, in the theory of measurement errors. It is on the basis of the theory of measurement errors that the normal law was first substantiated by Laplace and Gauss. Indeed, in most cases, errors arising from the measurement of tex or other physical quantities are distributed according to the normal law; The reason for this is that such errors, as a rule, are made up of numerous independent elementary errors caused by various causes. For a long time, normal law was considered the only and universal law of error. At present, the view of a normal law as the only one and universal should be revised (experience shows that in a number of measurement and production processes there are distribution laws that are different from normal), but still the normal law remains the most common and most important law for practice .