Lecture
Present 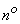 We will consider one of the questions related to the verification of the likelihood of hypotheses, namely, the question of the consistency of the theoretical and statistical distribution.
We will consider one of the questions related to the verification of the likelihood of hypotheses, namely, the question of the consistency of the theoretical and statistical distribution.
Assume that this statistical distribution is aligned with the help of some theoretical curve 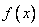 (fig. 7.6.1). No matter how well the theoretical curve is chosen, some discrepancies are inevitable between it and the statistical distribution. Naturally, the question arises: are these differences explained only by random circumstances associated with a limited number of observations, or are they significant and related to the fact that the curve we have chosen does not evenly align this statistical distribution? To answer this question are the so-called "criteria of consent."
(fig. 7.6.1). No matter how well the theoretical curve is chosen, some discrepancies are inevitable between it and the statistical distribution. Naturally, the question arises: are these differences explained only by random circumstances associated with a limited number of observations, or are they significant and related to the fact that the curve we have chosen does not evenly align this statistical distribution? To answer this question are the so-called "criteria of consent."
The idea of applying acceptance criteria is as follows.
Based on this statistical material we have to test the hypothesis 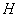 consisting in that random variable
consisting in that random variable 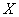 obeys some definite law of distribution. This law can be specified in one form or another: for example, as a distribution function
obeys some definite law of distribution. This law can be specified in one form or another: for example, as a distribution function 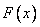 or as a distribution density
or as a distribution density 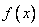 or in the form of a set of probabilities
or in the form of a set of probabilities 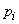 where
where 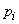 - the probability that the magnitude
- the probability that the magnitude 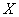 will fall into the limits
will fall into the limits 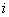 th discharge.
th discharge.
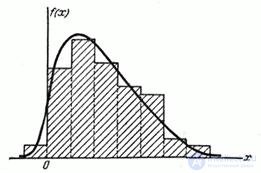
Fig. 7.6.1
Since of these forms, the distribution function 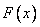 is the most common and defines any other, we will formulate a hypothesis
is the most common and defines any other, we will formulate a hypothesis 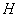 as consisting in that magnitude
as consisting in that magnitude 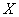 has a distribution function
has a distribution function 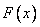 .
.
In order to accept or disprove the hypothesis 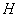 consider some value
consider some value  characterizing the degree of discrepancy between the theoretical and statistical distributions. Magnitude
characterizing the degree of discrepancy between the theoretical and statistical distributions. Magnitude  can be selected in various ways; for example, as
can be selected in various ways; for example, as  you can take the sum of the squares of the deviations of theoretical probabilities
you can take the sum of the squares of the deviations of theoretical probabilities 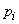 from relevant frequencies
from relevant frequencies 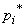 or the sum of the same squares with some coefficients ("weights"), or the maximum deviation of the statistical distribution function
or the sum of the same squares with some coefficients ("weights"), or the maximum deviation of the statistical distribution function 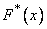 from theoretical
from theoretical 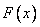 etc. Let us assume that the quantity
etc. Let us assume that the quantity 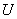 selected one way or another. Obviously, this is some random variable. The distribution law of this random variable depends on the distribution law of the random variable.
selected one way or another. Obviously, this is some random variable. The distribution law of this random variable depends on the distribution law of the random variable. 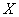 over which experiments were made, and on the number of experiments
over which experiments were made, and on the number of experiments 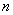 . If hypothesis
. If hypothesis 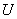 true, then the distribution law
true, then the distribution law 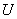 determined by the law of distribution of magnitude
determined by the law of distribution of magnitude 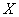 (function
(function 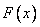 ) and number
) and number 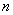 .
.
Suppose that this distribution law is known to us. As a result of this series of experiments, it was found that the chosen measure of discrepancy 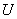 took some meaning
took some meaning 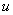 . The question is whether this can be explained by random reasons or is this discrepancy too great and indicates the presence of a significant difference between the theoretical and statistical distributions and, consequently, the unsuitability of the hypothesis
. The question is whether this can be explained by random reasons or is this discrepancy too great and indicates the presence of a significant difference between the theoretical and statistical distributions and, consequently, the unsuitability of the hypothesis  ? To answer this question, suppose the hypothesis
? To answer this question, suppose the hypothesis  is correct, and we calculate in this assumption the probability that the hypothesis
is correct, and we calculate in this assumption the probability that the hypothesis  is correct, and we calculate in this assumption the probability that due to random reasons associated with an insufficient amount of experimental material, the measure of discrepancy
is correct, and we calculate in this assumption the probability that due to random reasons associated with an insufficient amount of experimental material, the measure of discrepancy 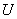 will be no less than the value we observed in the experiment
will be no less than the value we observed in the experiment 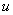 , i.e., we calculate the probability of an event:
, i.e., we calculate the probability of an event:
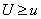 .
.
If this probability is very small, then the hypothesis 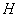 should reject as little believable; if this probability is significant, it should be recognized that the experimental data do not contradict the hypothesis
should reject as little believable; if this probability is significant, it should be recognized that the experimental data do not contradict the hypothesis 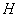 .
.
The question arises of how to choose the measure of discrepancy. 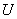 ? It turns out that with some ways of choosing it, the distribution law
? It turns out that with some ways of choosing it, the distribution law 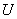 has very simple properties with a sufficiently large
has very simple properties with a sufficiently large 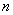 practically independent of function
practically independent of function 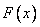 . It is precisely such measures that discrepancies use in mathematical statistics as criteria for agreement.
. It is precisely such measures that discrepancies use in mathematical statistics as criteria for agreement.
Consider one of the most commonly used criteria of consent - the so-called "criterion  Pearson.
Pearson.
Suppose that produced 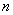 independent experiments, in each of which a random variable
independent experiments, in each of which a random variable 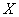 took a certain meaning. The results of the experiments are summarized in
took a certain meaning. The results of the experiments are summarized in 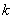 discharges and decorated in the form of statistical series:
discharges and decorated in the form of statistical series:
|
|
|
|
|
|
|
|
|
|
It is required to check whether the experimental data are consistent with the hypothesis that the random variable 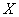 has a given distribution law (given by the distribution function
has a given distribution law (given by the distribution function 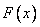 or density
or density 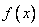 ). Let's call this distribution law “theoretical”.
). Let's call this distribution law “theoretical”.
Knowing the distribution law, one can find the theoretical probabilities of a random variable falling into each of the digits:
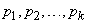 .
.
Checking the consistency of the theoretical and statistical distributions, we will proceed from the discrepancies between the theoretical probabilities 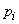 and observed frequencies
and observed frequencies 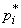 . It is natural to choose as a measure of the discrepancy between the theoretical and statistical distributions the sum of squared deviations
. It is natural to choose as a measure of the discrepancy between the theoretical and statistical distributions the sum of squared deviations 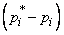 taken with some weights
taken with some weights 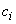 :
:
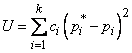 . (7.6.1)
. (7.6.1)
Coefficients 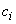 (“Weights” of digits) are introduced because, in the general case, deviations related to different digits cannot be considered equal in importance. Indeed, the same in absolute value deviation
(“Weights” of digits) are introduced because, in the general case, deviations related to different digits cannot be considered equal in importance. Indeed, the same in absolute value deviation 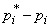 may be of little significance if the probability itself
may be of little significance if the probability itself 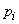 is small. Therefore, of course "weight"
is small. Therefore, of course "weight" 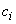 take back proportional to the probabilities of discharges
take back proportional to the probabilities of discharges 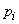 .
.
The next question is how to choose the coefficient of proportionality.
K. Pearson showed that if we put
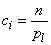 (7.6.2)
(7.6.2)
then for large 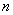 distribution law
distribution law 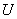 It has very simple properties: it practically does not depend on the distribution function
It has very simple properties: it practically does not depend on the distribution function 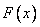 and on the number of experiences
and on the number of experiences 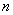 namely, this law when increasing
namely, this law when increasing 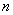 approaching the so-called “distribution
approaching the so-called “distribution  ".
".
With this choice of coefficients 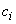 measure of discrepancy is usually denoted
measure of discrepancy is usually denoted  :
:
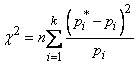 . (7.6.3)
. (7.6.3)
For ease of calculation (to avoid dealing with fractional values with a large number of zeros), you can enter 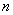 under the sum sign and given that
under the sum sign and given that 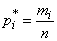 where
where 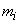 - the number of values in
- the number of values in 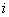 th discharge, bring the formula (7.6.3) to the form:
th discharge, bring the formula (7.6.3) to the form:
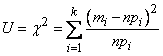 (7.6.4)
(7.6.4)
Distribution  depends on parameter
depends on parameter 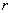 , called the number of "degrees of freedom" distribution. The number of "degrees of freedom"
, called the number of "degrees of freedom" distribution. The number of "degrees of freedom" 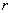 equal to the number of digits
equal to the number of digits 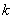 minus the number of independent conditions ("connections") imposed on the frequencies
minus the number of independent conditions ("connections") imposed on the frequencies 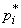 . Examples of such conditions can be
. Examples of such conditions can be
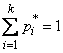 ,
,
if we require only that the sum of frequencies be equal to one (this requirement is imposed in all cases);
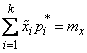 ,
,
if we select a theoretical distribution with the condition that the theoretical and statistical averages coincide;
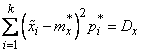 ,
,
if we also require a coincidence of theoretical and statistical variances, etc.
For distribution  compiled tables (see table. 4 annex). Using these tables, you can for each value
compiled tables (see table. 4 annex). Using these tables, you can for each value  and numbers of degrees of freedom
and numbers of degrees of freedom 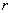 find probability
find probability 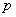 the fact that the value distributed by law
the fact that the value distributed by law  will surpass this value. In tab. 4 inputs are: probability value
will surpass this value. In tab. 4 inputs are: probability value 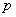 and the number of degrees of freedom
and the number of degrees of freedom 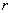 . The numbers in the table represent the corresponding values.
. The numbers in the table represent the corresponding values.  .
.
Distribution  It makes it possible to assess the degree of consistency of the theoretical and statistical distributions. We will proceed from the fact that
It makes it possible to assess the degree of consistency of the theoretical and statistical distributions. We will proceed from the fact that 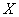 really distributed by law
really distributed by law 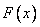 . Then the probability
. Then the probability 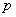 , determined by the table, there is a probability that, due to purely random reasons, the measure of the discrepancy between the theoretical and statistical distributions (7.6.4) will be no less than that actually observed in this series of experiments
, determined by the table, there is a probability that, due to purely random reasons, the measure of the discrepancy between the theoretical and statistical distributions (7.6.4) will be no less than that actually observed in this series of experiments  . If this probability
. If this probability 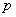 very small (so small that an event with such a probability can be considered almost impossible), the result of the experiment should be considered contrary to the hypothesis
very small (so small that an event with such a probability can be considered almost impossible), the result of the experiment should be considered contrary to the hypothesis 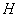 that the law of distribution of magnitude
that the law of distribution of magnitude 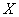 there is
there is 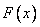 . This hypothesis should be discarded as implausible. On the contrary, if the probability
. This hypothesis should be discarded as implausible. On the contrary, if the probability 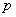 relatively large, it is possible to recognize the discrepancies between the theoretical and statistical distributions insignificant and attributed to them due to random reasons. Hypothesis
relatively large, it is possible to recognize the discrepancies between the theoretical and statistical distributions insignificant and attributed to them due to random reasons. Hypothesis 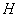 that magnitude
that magnitude 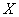 distributed by law
distributed by law 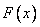 , can be considered plausible or, at least, not contrary to experimental data.
, can be considered plausible or, at least, not contrary to experimental data.
Thus, the application of the criterion  to assessing the consistency of the theoretical and statistical distributions comes down to the following:
to assessing the consistency of the theoretical and statistical distributions comes down to the following:
1) The measure of discrepancy is determined.  according to the formula (7.6.4).
according to the formula (7.6.4).
2) The number of degrees of freedom is determined. 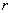 as the number of digits
as the number of digits 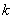 minus the number of superimposed connections
minus the number of superimposed connections 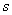 :
:
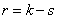 .
.
3) By 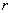 and
and  using table. 4 determines the probability that the quantity having the distribution
using table. 4 determines the probability that the quantity having the distribution  with
with 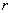 degrees of freedom that exceed this value
degrees of freedom that exceed this value  . If this probability is very small, the hypothesis is rejected as implausible. If this probability is relatively large, the hypothesis can be considered not contradicting the experimental data.
. If this probability is very small, the hypothesis is rejected as implausible. If this probability is relatively large, the hypothesis can be considered not contradicting the experimental data.
How low should the probability be 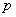 in order to discard or revise a hypothesis, the question is uncertain; it cannot be solved for mathematical reasons, as well as the question of how small the probability of an event must be in order to consider it practically impossible. In practice, if
in order to discard or revise a hypothesis, the question is uncertain; it cannot be solved for mathematical reasons, as well as the question of how small the probability of an event must be in order to consider it practically impossible. In practice, if 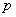 turns out to be less than 0.1, it is recommended to check the experiment, if possible - to repeat it and in case noticeable discrepancies reappear, trying to find a distribution law that is more suitable for describing statistical data.
turns out to be less than 0.1, it is recommended to check the experiment, if possible - to repeat it and in case noticeable discrepancies reappear, trying to find a distribution law that is more suitable for describing statistical data.
It should be noted that using the criterion  (or any other consent) it is possible only in some cases to refute the selected hypothesis
(or any other consent) it is possible only in some cases to refute the selected hypothesis 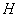 and discard it as clearly disagree with the experimental data - if the probability
and discard it as clearly disagree with the experimental data - if the probability 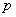 is great, this fact alone can by no means be considered proof of the validity of the hypothesis
is great, this fact alone can by no means be considered proof of the validity of the hypothesis 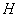 , and only indicates that the hypothesis does not contradict the experimental data.
, and only indicates that the hypothesis does not contradict the experimental data.
At first glance it may seem that the greater the probability p, the better the consistency of the theoretical and statistical distributions and the more justified the choice of function 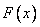 as a law of the distribution of a random variable. In fact, it is not. Assume, for example, that, evaluating the agreement of the theoretical and statistical distribution by the criterion
as a law of the distribution of a random variable. In fact, it is not. Assume, for example, that, evaluating the agreement of the theoretical and statistical distribution by the criterion  , we got
, we got 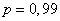 . This means that with a probability of 0.99 due to purely random reasons, with a given number of experiments, the discrepancies should be larger than the observed ones. We have received relatively very small discrepancies that are too small to recognize them as plausible. It is more reasonable to recognize that such a close coincidence of the theoretical and statistical distributions is not accidental and can be explained by certain reasons related to the registration and processing of experimental data (in particular, the “cleanup” of experimental data that is very common in practice, when some results are randomly discarded or several vary).
. This means that with a probability of 0.99 due to purely random reasons, with a given number of experiments, the discrepancies should be larger than the observed ones. We have received relatively very small discrepancies that are too small to recognize them as plausible. It is more reasonable to recognize that such a close coincidence of the theoretical and statistical distributions is not accidental and can be explained by certain reasons related to the registration and processing of experimental data (in particular, the “cleanup” of experimental data that is very common in practice, when some results are randomly discarded or several vary).
Of course, all these considerations are applicable only in cases where the number of experiments 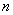 is large enough (of the order of a few hundred) and when it makes sense to apply the criterion itself, based on the limiting distribution of the measure of discrepancy when
is large enough (of the order of a few hundred) and when it makes sense to apply the criterion itself, based on the limiting distribution of the measure of discrepancy when 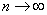 . Note that when using the criterion
. Note that when using the criterion  not only the total number of experiments should be large enough
not only the total number of experiments should be large enough 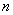 but the numbers of observations
but the numbers of observations 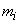 in separate ranks. In practice, it is recommended to have at least 5 to 10 observations in each digit. If the number of observations in individual bits is very small (of the order of 1 - 2), it makes sense to combine some bits.
in separate ranks. In practice, it is recommended to have at least 5 to 10 observations in each digit. If the number of observations in individual bits is very small (of the order of 1 - 2), it makes sense to combine some bits.
Example 1. Check consistency of theoretical and statistical distributions for example 1 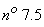 .
.
Decision. Using the theoretical normal distribution law with parameters
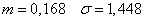 ,
,
find the probability of falling into the ranks by the formula
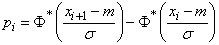 ,
,
Where 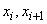 - boundaries
- boundaries 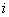 th discharge.
th discharge.
Then we make a comparative table of numbers of hits in the bits. 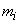 and corresponding values
and corresponding values 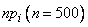 .
.
| –4; –3 | –3; –2 | –2; –1 | –1; 0 | 0; 1 | 1; 2 | 2; 3 | 3; 4 |
| 6 | 25 | 72 | 133 | 120 | 88 | 46 | ten |
| 6.2 | 26.2 | 71.2 | 122, | 131,8 | 90.5 | 38.5 | 10.5 |
According to the formula (7.6.4) determine the value of the measure of discrepancy

We determine the number of degrees of freedom as the number of digits minus the number of superimposed bonds. 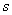 (in this case
(in this case 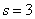 ):
):
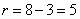 .
.
According to the table. 4 applications we find for 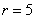 :
:
at 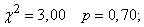
at 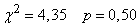 .
.
Therefore, the desired probability 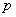 at
at 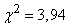 approximately equal to 0.56.This probability is not small; therefore, the hypothesis that the value is
approximately equal to 0.56.This probability is not small; therefore, the hypothesis that the value is 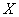 distributed according to the normal law can be considered plausible.
distributed according to the normal law can be considered plausible.
Example 2. Check the consistency of the theoretical and statistical distributions for the conditions of example 2  7.5.
7.5.
Decision. Meanings 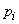 we calculate as probabilities of hitting the sections (20; 30). (30; 40), etc. for a random variable distributed according to the law of uniform density on a segment (23.6; 96.6). We make a comparative table of values
we calculate as probabilities of hitting the sections (20; 30). (30; 40), etc. for a random variable distributed according to the law of uniform density on a segment (23.6; 96.6). We make a comparative table of values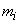 and
and 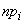
 :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
By the formula (7.6.4) we find  :
:

The number of degrees of freedom:
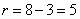
According to the table. 4 applications we have:
at 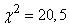 and
and 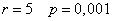 .
.
Consequently, the discrepancy observed by us between the theoretical and statistical distributions could appear for purely random reasons only with probability. 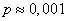 .Since this probability is very small, it should be recognized that the experimental data contradict the hypothesis that the value is
.Since this probability is very small, it should be recognized that the experimental data contradict the hypothesis that the value is 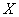 distributed according to the law of uniform density.
distributed according to the law of uniform density.
In addition to the criterion  , a number of other criteria are used in practice to assess the degree of consistency of the theoretical and statistical distributions. Of these, we briefly discuss the criteria of A.N. Kolmogorov.
, a number of other criteria are used in practice to assess the degree of consistency of the theoretical and statistical distributions. Of these, we briefly discuss the criteria of A.N. Kolmogorov.
As a measure of the discrepancy between the theoretical and statistical distributions, A.N. Kolmogorov considers the maximum modulus of the difference between the statistical distribution function 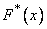 and the corresponding theoretical distribution function:
and the corresponding theoretical distribution function:
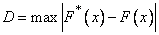 .
.
The basis for choosing as a measure of the divergence of the value  is the simplicity of its calculation. At the same time, it has a fairly simple distribution law. A. N. Kolmogorov proved that, whatever the distribution function of a
is the simplicity of its calculation. At the same time, it has a fairly simple distribution law. A. N. Kolmogorov proved that, whatever the distribution function of a  continuous random variable
continuous random variable  , with an unlimited increase in the number of independent observations
, with an unlimited increase in the number of independent observations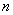 probability of inequality
probability of inequality
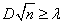
tends to the limit
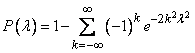 (7.6.5)
(7.6.5)
The probability values 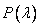 calculated by the formula
calculated by the formula 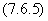 are given in table 7.6.1.
are given in table 7.6.1.
|
|
|
|
|
|
|
|
|
|
|
|
The scheme of application of the criterion A.N. Kolmogorov is as follows: a statistical distribution function 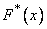 and an estimated theoretical distribution function are constructed
and an estimated theoretical distribution function are constructed 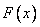 , and the maximum
, and the maximum 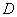 modulus of the difference between them is determined (Fig. 7.6.2).
modulus of the difference between them is determined (Fig. 7.6.2).
Further, the determined value
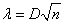
and table 7.6.1 is the probability 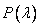 .This is the probability that (if the value is
.This is the probability that (if the value is 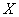 indeed distributed according to the law
indeed distributed according to the law 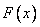 ) due to purely random reasons, the maximum discrepancy between
) due to purely random reasons, the maximum discrepancy between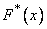 and
and 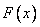 will be no less than actually observed. If the probability
will be no less than actually observed. If the probability 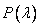 very small, the hypothesis should be rejected as implausible; at relatively large,
very small, the hypothesis should be rejected as implausible; at relatively large, 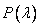 it can be considered compatible with the experimental data.
it can be considered compatible with the experimental data.
Fig. 7.6.2
Criterion A.N. Kolmogorov its simplicity favorably with the previously described criterion ;therefore, it is very readily applied in practice. However, it should be stipulated that this criterion can be applied only in the case when the hypothetical distribution is
;therefore, it is very readily applied in practice. However, it should be stipulated that this criterion can be applied only in the case when the hypothetical distribution is  completely known in advance from any theoretical considerations, i.e. when not only the type of distribution function is known
completely known in advance from any theoretical considerations, i.e. when not only the type of distribution function is known  , but also all parameters included in it. Such a case is relatively rare in practice. Usually, from theoretical considerations, only the general form of the function is known
, but also all parameters included in it. Such a case is relatively rare in practice. Usually, from theoretical considerations, only the general form of the function is known  , and the numerical parameters included in it are determined from the given statistical material. When applying the criterion,
, and the numerical parameters included in it are determined from the given statistical material. When applying the criterion,  this circumstance is taken into account by a corresponding decrease in the number of degrees of freedom of distribution.
this circumstance is taken into account by a corresponding decrease in the number of degrees of freedom of distribution. .Criterion A.N. Kolmogorov does not provide for such an agreement. If, however, this criterion is applied in cases where the parameters of the theoretical distribution are selected from statistical data, the criterion gives obviously high values of probability
.Criterion A.N. Kolmogorov does not provide for such an agreement. If, however, this criterion is applied in cases where the parameters of the theoretical distribution are selected from statistical data, the criterion gives obviously high values of probability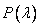 ; therefore, in some cases, we risk accepting as a plausible hypothesis, in reality, which does not agree well with experimental data.
; therefore, in some cases, we risk accepting as a plausible hypothesis, in reality, which does not agree well with experimental data.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis