Lecture
The well-known theorem of J. Bernoulli, which establishes a connection between the frequency of an event and its probability, can be proved as a direct consequence of the law of large numbers.
Let produced 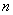 independent experiments, in each of which some event may or may not appear
independent experiments, in each of which some event may or may not appear 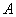 whose probability in every experience is equal
whose probability in every experience is equal 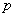 . Theorem J. Bernoulli argues that with an unlimited increase in the number of experiments
. Theorem J. Bernoulli argues that with an unlimited increase in the number of experiments 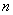 event frequency
event frequency 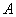 converges in probability to its probability
converges in probability to its probability 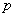 .
.
Denote the frequency of the event 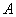 at
at 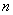 experiences through
experiences through 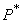 and we write down theorem J. Bernoulli as a formula
and we write down theorem J. Bernoulli as a formula
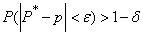 , (13.5.1)
, (13.5.1)
Where, 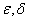 - arbitrarily small positive numbers.
- arbitrarily small positive numbers.
It is required to prove the validity of this formula for a sufficiently large 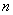 .
.
Evidence. Consider independent random variables:
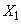 - the number of occurrences
- the number of occurrences 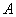 in the first experience;
in the first experience;
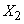 - the number of occurrences
- the number of occurrences 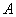 in the second experiment, etc.
in the second experiment, etc.
All these quantities are discontinuous and have the same distribution law, expressed by a series of the form:
|
|
|
|
Where 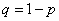 . The expectation of each of the values
. The expectation of each of the values 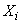 equally
equally 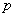 and its dispersion
and its dispersion 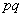 (cm.
(cm. 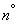 10.3).
10.3).
Frequency 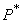 is nothing more than the arithmetic average of the values
is nothing more than the arithmetic average of the values 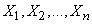 :
:
 ,
,
and, according to the law of large numbers, converges in probability to the total expectation of these random variables. Hence the inequality (13.5.1).
Theorem J. Bernoulli claims frequency stability under constant conditions of experience. But under changing conditions of experience, similar stability also exists. The theorem establishing the frequency stability property under varying conditions of experience is called the Poisson theorem and is formulated as follows:
If produced 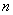 independent experiences and the likelihood of an event
independent experiences and the likelihood of an event 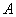 at
at 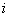 m experience is
m experience is 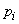 then increasing
then increasing 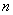 event frequency
event frequency 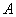 converges in probability to the arithmetic mean of the probabilities
converges in probability to the arithmetic mean of the probabilities 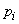 .
.
The Poisson theorem is derived from the generalized Chebyshev theorem in the same way as the Bernoulli theorem was derived from the law of large numbers.
The Poisson theorem is of great fundamental importance for the practical application of probability theory. The fact is that probabilistic methods are often used to study phenomena that, under the same conditions, do not have a chance to repeat themselves many times, but repeat many times under very diverse conditions, and the probabilities of events of interest to us strongly depend on these conditions. For example, the probability of hitting a target in an air battle essentially depends on the firing range, the angle of the target, the altitude, the speed of the shooting aircraft and the target, etc. fixed terms. And yet, despite this, in this phenomenon there is a certain stability of frequencies, namely the frequency of hitting the target in real air battles, carried out in a variety of conditions, will approach the average probability of hitting the target, characteristic of this group of conditions. Therefore, those methods of organizing shooting, which are based on the maximum probability of hitting the target, will be justified in this case, despite the fact that one cannot expect a true mass character of the experiments in each specific set of conditions.
The situation is similar in the field of experimental verification of probabilistic calculations. In practice, it is often the case that it is necessary to test by experience the correspondence of the calculated probability of an event. 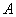 its actual frequency. Most often this is done in order to verify the correctness of one or another theoretical scheme underlying the method for calculating the probability of an event. Often, with such experimental verification, it is not possible to reproduce the same experimental conditions many times. Nevertheless, this verification can be carried out if we compare the observed frequency in an experiment not with its probability for fixed conditions, but with the arithmetic mean of the probabilities calculated for various conditions.
its actual frequency. Most often this is done in order to verify the correctness of one or another theoretical scheme underlying the method for calculating the probability of an event. Often, with such experimental verification, it is not possible to reproduce the same experimental conditions many times. Nevertheless, this verification can be carried out if we compare the observed frequency in an experiment not with its probability for fixed conditions, but with the arithmetic mean of the probabilities calculated for various conditions.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis