Lecture
By constructing the spectral decomposition of a stationary random function 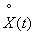 on the final time segment
on the final time segment 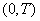 , we obtained the spectrum of variances of a random function in the form of a series of separate discrete lines, separated by equal intervals (the so-called "discontinuous" or "ruled" spectrum).
, we obtained the spectrum of variances of a random function in the form of a series of separate discrete lines, separated by equal intervals (the so-called "discontinuous" or "ruled" spectrum).
Obviously, the more time we consider, the more complete will be our information about the random function. It is therefore natural in the spectral decomposition to try to go to the limit at 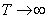 and see what happens to the spectrum of a random function. With
and see what happens to the spectrum of a random function. With 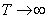
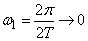 ; so the distances between frequencies
; so the distances between frequencies 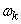 on which the spectrum is built, will be at
on which the spectrum is built, will be at 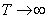 unlimited decrease. In this case, the discrete spectrum will approach a continuous one, in which each arbitrarily small frequency interval
unlimited decrease. In this case, the discrete spectrum will approach a continuous one, in which each arbitrarily small frequency interval 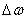 will match the elementary variance
will match the elementary variance 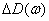 .
.
Let's try to draw a continuous spectrum graphically. To do this, we must somewhat rearrange the graph of the discrete spectrum at a finite 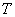 . Namely, we will postpone the ordinate no longer the variance
. Namely, we will postpone the ordinate no longer the variance 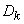 (which decreases infinitely with
(which decreases infinitely with 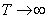 ), and the mean density of dispersion, i.e., the dispersion per unit length of a given frequency interval. Denote the distance between adjacent frequencies.
), and the mean density of dispersion, i.e., the dispersion per unit length of a given frequency interval. Denote the distance between adjacent frequencies. 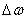 :
:
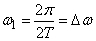
and at each segment 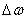 as on the base, we construct a rectangle with an area
as on the base, we construct a rectangle with an area 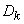 (fig. 17.3.1). We obtain a step diagram that resembles a histogram of a statistical distribution on the basis of its construction.
(fig. 17.3.1). We obtain a step diagram that resembles a histogram of a statistical distribution on the basis of its construction.
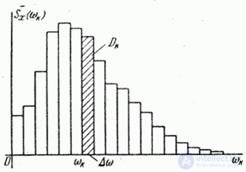
Fig. 17.3.1.
Chart height on the plot 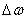 adjacent to the point
adjacent to the point 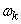 equal to
equal to
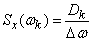 (17.3.1)
(17.3.1)
and represents the average dispersion density in this region.
The total area of the whole diagram is obviously equal to the variance of the random function.
We will indefinitely increase the interval 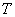 . Wherein
. Wherein 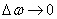 and the stepped curve will approach the smooth curve indefinitely
and the stepped curve will approach the smooth curve indefinitely 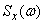 (fig. 17.3.2). This curve depicts the dispersion density of the continuous spectrum frequencies, and the function itself
(fig. 17.3.2). This curve depicts the dispersion density of the continuous spectrum frequencies, and the function itself 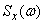 called the spectral density of the dispersion, or, in short, the spectral density of the stationary random function
called the spectral density of the dispersion, or, in short, the spectral density of the stationary random function  .
.
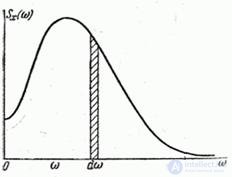
Fig. 17.3.2.
Obviously, the area bounded by the curve 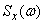 , must still be equal to the variance
, must still be equal to the variance 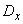 random function
random function 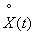 :
:
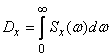 . (17.3.2)
. (17.3.2)
Formula (17.3.2) is nothing more than decomposition of the variance. 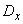 for the sum of elementary terms
for the sum of elementary terms 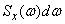 , each of which is a dispersion per elementary frequency band
, each of which is a dispersion per elementary frequency band 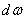 adjacent to the point
adjacent to the point 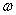 (fig. 17.3.2).
(fig. 17.3.2).
Thus, we have introduced a new additional characteristic of a stationary random process - the spectral density, which describes the frequency composition of the stationary process. However, this characteristic is not independent; it is completely determined by the correlation function of this process. Just as the ordinates of the discrete spectrum 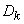 expressed by formulas (17.2.4) through the correlation function
expressed by formulas (17.2.4) through the correlation function 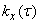 spectral density
spectral density 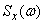 can also be expressed through the correlation function.
can also be expressed through the correlation function.
We derive this expression. To do this, we proceed in the canonical expansion of the correlation function to the limit at 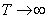 and see what it turns into. We will proceed from the decomposition (17.2.1) of the correlation function in a Fourier series on a finite interval
and see what it turns into. We will proceed from the decomposition (17.2.1) of the correlation function in a Fourier series on a finite interval 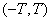 :
:
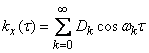 , (17.3.3)
, (17.3.3)
where is the variance corresponding to the frequency 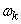 expressed by the formula
expressed by the formula
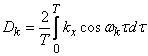 . (17.3.4)
. (17.3.4)
Before moving to the limit at 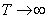 Let us turn to the formula (17.3.3) from the variance
Let us turn to the formula (17.3.3) from the variance 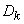 to average dispersion density
to average dispersion density 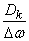 . Since this density is calculated even at a finite value
. Since this density is calculated even at a finite value 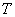 and depends on
and depends on 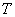 , we denote it:
, we denote it:
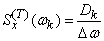 . (17.3.5)
. (17.3.5)
Divide expression (17.3.4) by 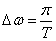 ; we will receive:
; we will receive:
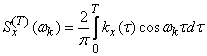 . (17.3.6)
. (17.3.6)
From (17.3.5) it follows that
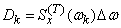 . (17.3.7)
. (17.3.7)
Substitute the expression (17.3.7) into the formula (17.3.3); we will receive:
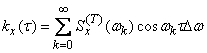 . (17.3.8)
. (17.3.8)
Let's see what expression (17.3.8) will turn into 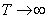 . Obviously, while
. Obviously, while 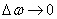 ; discrete argument
; discrete argument 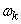 turns into a continuously changing argument
turns into a continuously changing argument 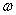 ; the sum goes to the integral of the variable
; the sum goes to the integral of the variable 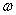 ; average dispersion density
; average dispersion density 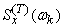 tends to dispersion density
tends to dispersion density 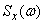 , and the expression (17.3.8) in the limit takes the form:
, and the expression (17.3.8) in the limit takes the form:
 , (17.3.9)
, (17.3.9)
Where 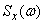 - spectral density of a stationary random function.
- spectral density of a stationary random function.
Going to the limit at 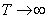 in the formula (17.3.6), we obtain the expression of the spectral density through the correlation function:
in the formula (17.3.6), we obtain the expression of the spectral density through the correlation function:
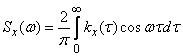 . (17.3.10)
. (17.3.10)
An expression of the type (17.3.9) is known in mathematics as the Fourier integral. The Fourier integral is a generalization of the expansion in a Fourier series for the case of a non-periodic function considered on an infinite interval, and is a decomposition of a function into a sum of elementary harmonic oscillations with a continuous spectrum.
Just as the Fourier series expresses a decomposable function in terms of the coefficients of the series, which in turn are expressed in terms of the decomposable function, formulas (17.3.9) and (17.3.10) express functions 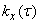 and
and 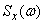 mutually: one over the other. The formula (17.3.9) expresses the correlation function in terms of spectral density; the formula (17.3.10), on the contrary, expresses the spectral density through the correlation function. Formulas of type (17.3.9) and (17.3.10) connecting mutually two functions are called Fourier transforms.
mutually: one over the other. The formula (17.3.9) expresses the correlation function in terms of spectral density; the formula (17.3.10), on the contrary, expresses the spectral density through the correlation function. Formulas of type (17.3.9) and (17.3.10) connecting mutually two functions are called Fourier transforms.
Thus, the correlation function and spectral density are expressed one through the other using Fourier transforms.
Note that from the general formula (17.3.9) with 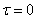 we obtain the previously obtained decomposition in frequency (17.3.2).
we obtain the previously obtained decomposition in frequency (17.3.2).
In practice, instead of spectral density 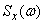 often use the normalized spectral density:
often use the normalized spectral density:
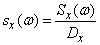 , (17.3.11)
, (17.3.11)
Where 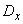 - variance of a random function.
- variance of a random function.
It is easy to verify that the normalized correlation function 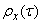 and normalized spectral density
and normalized spectral density 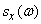 connected by the same Fourier transforms:
connected by the same Fourier transforms:
 (03/17/12)
(03/17/12)
Assuming in the first of equalities (17.3.12) 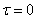 and considering that
and considering that 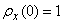 , we have:
, we have:
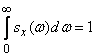 , (17.3.13)
, (17.3.13)
that is, the total area bounded by the graph of the normalized spectral density is equal to one.
Example 1. Normalized correlation function 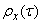 random function
random function 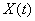 linearly decreasing from one to zero with
linearly decreasing from one to zero with 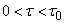 ; at
; at 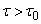
 (fig. 17.3.3).
(fig. 17.3.3).
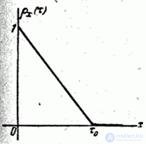
Fig. 17.3.3.
Determine the normalized spectral density of a random function 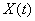 .
.
Decision. The normalized correlation function is expressed by the formulas:
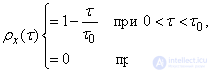
From the formulas (17.3.12) we have:
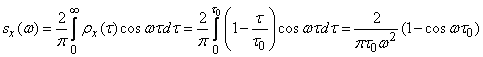 .
.
The graph of the normalized spectral density is presented in Fig. 17.3.4.
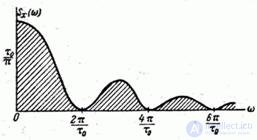
Fig. 17.3.4.
The first - the absolute - maximum spectral density is reached at 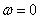 ; By disclosing uncertainty at this point, make sure that it is equal to
; By disclosing uncertainty at this point, make sure that it is equal to 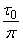 . Further, with increasing
. Further, with increasing 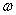 spectral density reaches a number of relative maxima, whose height decreases with increasing
spectral density reaches a number of relative maxima, whose height decreases with increasing 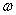 at
at 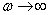
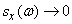 .
.
The nature of the change in spectral density 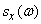 (fast or slow decay) depends on the parameter
(fast or slow decay) depends on the parameter 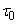 . Full area bounded by the curve
. Full area bounded by the curve 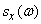 , is constant and equal to one. Change
, is constant and equal to one. Change 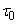 tantamount to changing the scale of the curve
tantamount to changing the scale of the curve 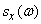 on both axes while maintaining its area. By increasing
on both axes while maintaining its area. By increasing 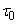 the scale on the ordinate axis increases, on the abscissa axis - decreases; the predominance of zero frequency in the spectrum of a random function becomes more pronounced. In the limit at
the scale on the ordinate axis increases, on the abscissa axis - decreases; the predominance of zero frequency in the spectrum of a random function becomes more pronounced. In the limit at 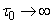 the random function degenerates into a normal random variable; wherein
the random function degenerates into a normal random variable; wherein 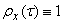 and the spectrum becomes discrete with a single frequency
and the spectrum becomes discrete with a single frequency 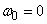 .
.
Example 2. Normalized spectral density 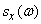 random function
random function 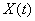 constant over a certain frequency range
constant over a certain frequency range 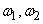 and is equal to zero outside this interval (fig. 17.3.5).
and is equal to zero outside this interval (fig. 17.3.5).
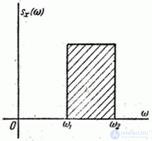
Fig. 17.3.5.
Determine the normalized correlation function of a random function 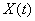 .
.
Decision. Value 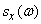 at
at 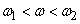 determined from the condition that the area bounded by the curve
determined from the condition that the area bounded by the curve 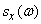 , is equal to one:
, is equal to one:
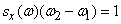 ,
, 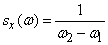 .
.
From (17.3.12) we have:
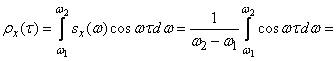
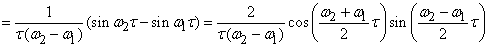 .
.
General view of the function 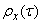 shown in fig. 17.3.6.
shown in fig. 17.3.6.
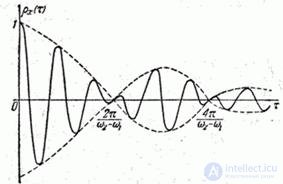
Fig. 17.3.6.
It has the character of oscillations decreasing in amplitude with a number of nodes at which the function vanishes. The specific type of graph obviously depends on the values 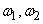 .
.
Of interest is the limiting view of the function. 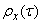 at
at 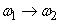 . Obviously when
. Obviously when 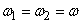 the spectrum of a random function is discrete with a single line corresponding to the frequency
the spectrum of a random function is discrete with a single line corresponding to the frequency 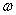 ; at the same time, the correlation function turns into a simple cosine wave:
; at the same time, the correlation function turns into a simple cosine wave:
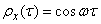 .
.
Let's see what kind of random function itself has in this case. 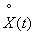 . With a discrete spectrum with a single line, the spectral decomposition of a stationary random function
. With a discrete spectrum with a single line, the spectral decomposition of a stationary random function 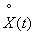 has the form:
has the form:
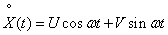 , (17.3.14)
, (17.3.14)
Where 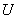 and
and 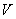 - uncorrelated random variables with a mathematical expectation of zero and equal variances:
- uncorrelated random variables with a mathematical expectation of zero and equal variances:
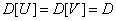 .
.
Let us show that a random function of the type (17.3.14) can be represented as one harmonic oscillation frequency 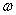 with random amplitude and random phase. Denoting
with random amplitude and random phase. Denoting
 ,
, 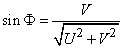 ,
,
we bring the expression (17.3.14) to the form:
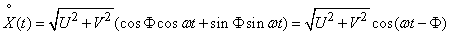 .
.
In this expression 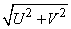 , the random amplitude;
, the random amplitude; 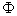 - random phase of harmonic oscillation.
- random phase of harmonic oscillation.
So far, we have considered only the case when the distribution of dispersions in frequencies is continuous, that is, when an infinitesimally small dispersion falls on an infinitesimal portion of frequencies. In practice, sometimes there are cases when a random function has in its composition a purely periodic frequency component 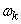 with a random amplitude. Then, in the spectral decomposition of a random function, in addition to the continuous spectrum of frequencies, there will also be a separate frequency
with a random amplitude. Then, in the spectral decomposition of a random function, in addition to the continuous spectrum of frequencies, there will also be a separate frequency 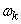 with a finite variance
with a finite variance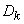 .In general, there may be several such periodic components. Then the spectral decomposition of the correlation function will consist of two parts: the discrete and continuous spectrum:
.In general, there may be several such periodic components. Then the spectral decomposition of the correlation function will consist of two parts: the discrete and continuous spectrum:
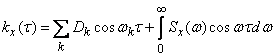 . (03/17/15)
. (03/17/15)
Cases of stationary random functions with such a “mixed” spectrum are rather rare in practice. In these cases, it always makes sense to divide the random function into two terms — with a continuous and discrete spectrum — and examine these terms separately.
Relatively often we have to deal with a special case when the final dispersion in the spectral decomposition of a random function falls at zero frequency ( 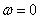 ). This means that a random variable with variance is included as part of the random function.
). This means that a random variable with variance is included as part of the random function. 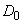 . In such cases, it also makes sense to select this random term and operate with it separately.
. In such cases, it also makes sense to select this random term and operate with it separately.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis