Lecture
Bernoulli's formula is convenient for calculations with only a relatively small number of tests. 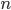 . For large values
. For large values 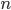 use the formula uncomfortable. Most often, in these cases, the Poisson formula is used. By the way, this formula is determined by the Poisson theorem.
use the formula uncomfortable. Most often, in these cases, the Poisson formula is used. By the way, this formula is determined by the Poisson theorem.
Note that the theorem. If the probability 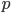 event occurrence
event occurrence 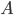 in each test is constant and small, and the number of independent tests
in each test is constant and small, and the number of independent tests 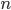 large enough, the probability of an event
large enough, the probability of an event 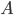 smooth
smooth 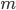 times approximately equal
times approximately equal
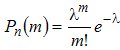 , (3.4)
, (3.4)
Where 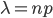 .
.
Evidence. Let given the probability of occurrence 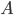 in one test
in one test 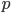 and the number of independent trials
and the number of independent trials 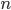 . Denote
. Denote 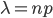 . Where p = λ / n
. Where p = λ / n 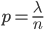 . Substitute ϶ᴛᴏ expression in the Bernoulli formula:
. Substitute ϶ᴛᴏ expression in the Bernoulli formula:
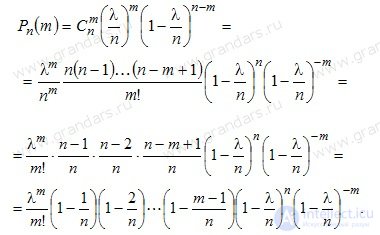
For a sufficiently large !! n ,, and relatively small !! m ,, all brackets, with the exception of the penultimate one, can be taken equal to one, i.e.
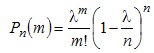
Given that n is sufficiently large, the right side of this expression can be considered when n-> oo, i.e. find limit
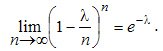
Then we get
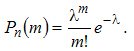 (3.5)
(3.5)
Example. The company manufactured and sent to the customer 100,000 bottles of beer. The likelihood that a bottle might be a bat is 0.0001. Find the probability that there will be exactly three and exactly five broken bottles in the shipment.
Decision. Given: n = 100000, p = 0.0001, m = 3 (m = 5).
Find 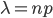 = 10
= 10
We use the Poisson formula
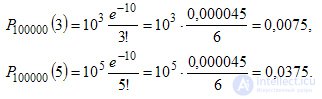
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis