Lecture
Let the input of a linear system with an operator 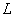 affect random function
affect random function 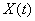 , and its characteristics are known: expectation
, and its characteristics are known: expectation 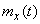 and correlation function
and correlation function 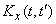 . The system response is a random function.
. The system response is a random function.
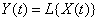 . (15.7.1)
. (15.7.1)
Required to find the characteristics of a random function  system output:
system output:  and
and 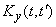 . In short: according to the characteristics of a random function at the input of a linear system, find the characteristics of a random function at the output.
. In short: according to the characteristics of a random function at the input of a linear system, find the characteristics of a random function at the output.
We first show that we can restrict ourselves to solving this problem only for a homogeneous operator.  . Indeed, let the operator
. Indeed, let the operator  heterogeneous and expressed by the formula
heterogeneous and expressed by the formula
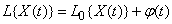 , (15.7.2)
, (15.7.2)
Where 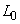 - linear homogeneous operator,
- linear homogeneous operator, 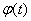 - a certain non-random function. Then
- a certain non-random function. Then
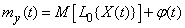 , (15.7.3)
, (15.7.3)
i.e. function 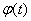 it is simply added to the expectation of a random function at the output of the linear system. As for the correlation function, then, as is known, it does not change from the addition of a non-random term to the random function.
it is simply added to the expectation of a random function at the output of the linear system. As for the correlation function, then, as is known, it does not change from the addition of a non-random term to the random function.
Therefore, in the following exposition, by “linear operators” we will understand only linear homogeneous operators.
We solve the problem of determining the characteristics at the output of a linear system first for some particular types of linear operators.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis