You get a bonus - 1 coin for daily activity. Now you have 1 coin

Random events Event algebra Classical and statistical definitions of the probability of an event

Lecture



In economics, as well as in other areas of human activity or in nature, one constantly has to deal with events that cannot be accurately predicted. Thus, the volume of sales of goods depends on demand, which can vary significantly, and on a number of other factors that are almost impossible to take into account. Therefore, when organizing production and sales, one has to predict the outcome of such activity based on either their own previous experience, or similar experience of other people, or intuition, which to a large extent also relies on experienced data.

In order to somehow evaluate the event in question, it is necessary to take into account or specially organize the conditions in which this event is recorded.

The implementation of certain conditions or actions to identify the event under consideration is called experience or experiment .

An event is called random if, as a result of experience, it may or may not occur.

An event is called authentic if it necessarily appears as a result of a given experience, and impossible if it cannot appear in this experience.

For example, snow falling in Moscow on November 30 is a random event. Daily sunrise can be considered a reliable event. Snowfall at the equator can be considered as an impossible event.

One of the main tasks in probability theory is the problem of determining the quantitative measure of the possibility of an event occurring.

Algebra of events

Sum of events 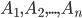Random events Event algebra Classical and statistical definitions of the probability of an event called the event consisting in the appearance of at least one of these events

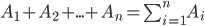
Random events Event algebra Classical and statistical definitions of the probability of an event

As an example, the sum of events can be called the presence in the store at least one of the two goods.

Event creation 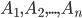Random events Event algebra Classical and statistical definitions of the probability of an event called an event consisting in the simultaneous occurrence of all these events

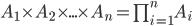
Random events Event algebra Classical and statistical definitions of the probability of an event

An event consisting in the appearance at the same time in the store of two goods is a product of events: 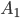Random events Event algebra Classical and statistical definitions of the probability of an event -the appearance of a single product, - 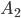Random events Event algebra Classical and statistical definitions of the probability of an event the appearance of another product.

Developments 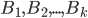Random events Event algebra Classical and statistical definitions of the probability of an event form a complete group of events, if at least one of them necessarily occurs in the experiment.

Example. The port has two berths for receiving ships. Three events can be considered: 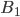Random events Event algebra Classical and statistical definitions of the probability of an event - absence of ships at berths, 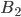Random events Event algebra Classical and statistical definitions of the probability of an event - the presence of one ship at one of the moorings, 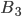Random events Event algebra Classical and statistical definitions of the probability of an event - the presence of two ships at two berths. These three events form a complete group of events.

Opposites are two unique events that make up the full group.

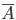If one of the events that are opposite, designate through Random events Event algebra Classical and statistical definitions of the probability of an event , then the opposite event is usually denoted by Random events Event algebra Classical and statistical definitions of the probability of an event .

Classical and statistical determination of the probability of an event

Each of the equally possible test results (experiments) is called an elementary outcome. They are usually denoted by letters. 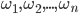Random events Event algebra Classical and statistical definitions of the probability of an event . For example, throws the dice. Elementary outcomes of all can be six by the number of points on the edges.

From elementary outcomes, you can make a more complex event. Thus, the event of loss of an even number of points is determined by three outcomes: 2, 4, 6.

A quantitative measure of the possibility of occurrence of the event under consideration is probability.

The most widely used are two definitions of the probability of an event: classical and statistical .

The classic definition of probability is associated with the notion of a favorable outcome.

The outcome is called favorable to this event, if its occurrence entails the occurrence of this event.

In the above example, the event in question - an even number of points on the dropped face, has three favorable outcomes. In this case, it is known and common
the number of possible outcomes. So, here you can use the classical definition of the probability of an event.

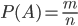The classic definition . Event probability Random events Event algebra Classical and statistical definitions of the probability of an event equals the ratio of the number of favorable outcomes to the total number of possible outcomes

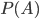Random events Event algebra Classical and statistical definitions of the probability of an event (1.1)

Where Random events Event algebra Classical and statistical definitions of the probability of an event - probability of an event Random events Event algebra Classical and statistical definitions of the probability of an event , Random events Event algebra Classical and statistical definitions of the probability of an event 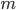- number of events favoring the event Random events Event algebra Classical and statistical definitions of the probability of an event outcomes 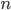Random events Event algebra Classical and statistical definitions of the probability of an event - the total number of possible outcomes.

In the considered example

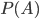Random events Event algebra Classical and statistical definitions of the probability of an event = 3/6 = 0.5

The statistical definition of probability is associated with the concept of the relative frequency of occurrence of an event. Random events Event algebra Classical and statistical definitions of the probability of an event in experiments.

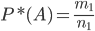Relative event frequency Random events Event algebra Classical and statistical definitions of the probability of an event calculated by the formula

Random events Event algebra Classical and statistical definitions of the probability of an event (1.2)

where m1   - the number of occurrences Random events Event algebra Classical and statistical definitions of the probability of an event in a series of n1 experiments (trials).

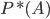Statistical definition . Probability of an event Random events Event algebra Classical and statistical definitions of the probability of an event is called the number relative to which the relative frequency is stabilized (established) Random events Event algebra Classical and statistical definitions of the probability of an event with an unlimited increase in the number of experiments.

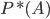In practical tasks for the probability of an event Random events Event algebra Classical and statistical definitions of the probability of an event relative frequency is taken Random events Event algebra Classical and statistical definitions of the probability of an event with a sufficiently large number of tests.

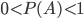
From these event probability definitions Random events Event algebra Classical and statistical definitions of the probability of an event it is clear that the inequality is always satisfied

Random events Event algebra Classical and statistical definitions of the probability of an event

To determine the probability of an event based on the formula (1.1), combinatorial formulas are often used, by which the number of favorable outcomes and the total number of possible outcomes are found.

Example. It is known that in the incoming batch of 30 sewing machines 10 have an internal defect. Determine the probability that from a batch of 5 at random, the taken 3 machines will prove to be defect-free.

Decision. To solve this problem, we introduce the notation. Let be 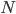Random events Event algebra Classical and statistical definitions of the probability of an event - the total number of machines, 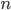Random events Event algebra Classical and statistical definitions of the probability of an event - the number of defect-free machines, 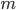Random events Event algebra Classical and statistical definitions of the probability of an event - the number of selected in a batch of machines, Random events Event algebra Classical and statistical definitions of the probability of an event - the number of defect-free machines in the selected batch.

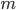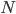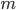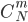Total number of combinations by Random events Event algebra Classical and statistical definitions of the probability of an event machines, i.e. the total number of possible outcomes will be equal to the number of combinations of Random events Event algebra Classical and statistical definitions of the probability of an event items by Random events Event algebra Classical and statistical definitions of the probability of an event i.e. Random events Event algebra Classical and statistical definitions of the probability of an event . But in each selected combination must contain three defect-free machines. 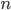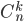The number of such combinations is equal to the number of combinations of Random events Event algebra Classical and statistical definitions of the probability of an event items by Random events Event algebra Classical and statistical definitions of the probability of an event i.e. Random events Event algebra Classical and statistical definitions of the probability of an event .

With each such combination in the selected batch, the remaining defective elements also form a set of combinations, the number of which is equal to the number of combinations of Nn elements by mk, i.e. 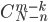Random events Event algebra Classical and statistical definitions of the probability of an event .

This means that the total number of favorable outcomes is determined by the product 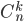Random events Event algebra Classical and statistical definitions of the probability of an event . Where do we get

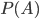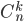
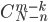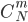
Random events Event algebra Classical and statistical definitions of the probability of an event = Random events Event algebra Classical and statistical definitions of the probability of an event Random events Event algebra Classical and statistical definitions of the probability of an event / Random events Event algebra Classical and statistical definitions of the probability of an event

Substitute in this formula the numerical values ​​of this example

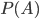Random events Event algebra Classical and statistical definitions of the probability of an event = ( C 2 0 ^ 3 * C 1 0 ^ 2) / C 3 0 ^ 5

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Probability theory. Mathematical Statistics and Stochastic Analysis

Terms: Probability theory. Mathematical Statistics and Stochastic Analysis