You get a bonus - 1 coin for daily activity. Now you have 1 coin

9.1. Normal law on the plane

Lecture



Of the laws of distribution of a system of two random variables, it makes sense to specifically consider the normal law as having the most widespread practice. Since a system of two random variables is depicted as a random point on a plane, the normal law for a system of two variables is often called the “normal” law on a plane.

In the general case, the density of the normal distribution of two random variables is expressed by the formula

9.1. Normal law on the plane . (9.1.1)

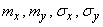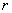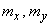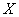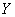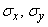This law depends on five parameters: 9.1. Normal law on the plane and 9.1. Normal law on the plane . The meaning of these parameters is easy to establish. Prove that the parameters 9.1. Normal law on the plane represent the mathematical expectation (centers of dispersion) values 9.1. Normal law on the plane and 9.1. Normal law on the plane ; 9.1. Normal law on the plane - their standard deviations; 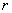9.1. 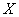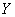Normal law on the plane - coefficient of correlation of quantities 9.1. Normal law on the plane and 9.1. Normal law on the plane .

In order to verify this, we first find the distribution density for each of the quantities in the system. According to the formula (8.4.2)

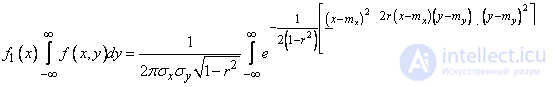9.1. Normal law on the plane .

Calculate the integral

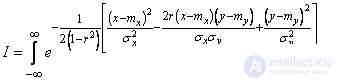9.1. Normal law on the plane .

Put:

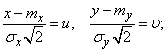9.1. Normal law on the plane (9.1.2)

then

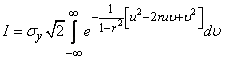9.1. Normal law on the plane .

From integral calculus it is known that

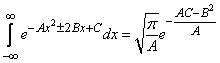9.1. Normal law on the plane . (9.1.3)

In our case

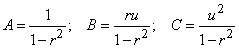9.1. Normal law on the plane .

Substituting these values ​​into the formula (9.1.3), we have:

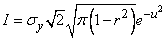9.1. Normal law on the plane ,

from where

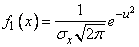9.1. Normal law on the plane ,

or, considering (9.1.2)

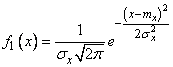9.1. Normal law on the plane . (9.1.4)

Thus, the magnitude 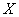9.1. Normal law on the plane subject to normal law with a dispersion center 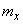9.1. Normal law on the plane and standard deviation 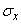9.1. Normal law on the plane . Similarly, we show that

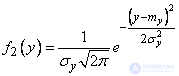9.1. Normal law on the plane , (9.1.5)

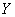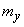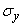those. magnitude 9.1. Normal law on the plane subject to normal law with a dispersion center 9.1. Normal law on the plane and standard deviation 9.1. Normal law on the plane .

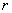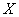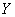It remains to prove that the parameter 9.1. Normal law on the plane in the formula (9.1.1) is the correlation coefficient of the quantities 9.1. Normal law on the plane and 9.1. Normal law on the plane . To do this, we calculate the correlation moment:

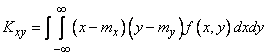9.1. Normal law on the plane ,

Where 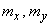9.1. Normal law on the plane - expected values 9.1. Normal law on the plane and 9.1. Normal law on the plane .

Substituting the expression in this formula 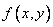9.1. Normal law on the plane , we get:

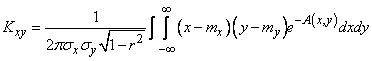9.1. Normal law on the plane , (9.1.6)

Where

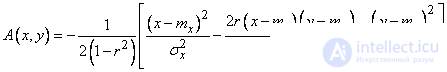9.1. Normal law on the plane .

We make in the double integral (9.1.6) the change of variables, putting:

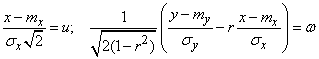9.1. Normal law on the plane . (9.1.7)

The conversion jacobian is

9.1. Normal law on the plane ,

Consequently,

9.1. Normal law on the plane

Considering that

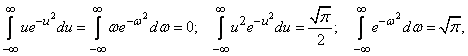
9.1. Normal law on the plane

we have:

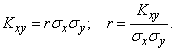9.1. Normal law on the plane (9.1.8)

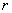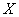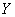Thus, it is proved that 9.1. Normal law on the plane in the formula (9.1.1) is the correlation coefficient of the quantities 9.1. Normal law on the plane and 9.1. Normal law on the plane .

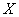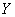Suppose now that random variables 9.1. Normal law on the plane and 9.1. Normal law on the plane , subordinate to the normal law on the plane, not correlated; we put in the formula (9.1.1) 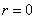9.1. Normal law on the plane . We get:

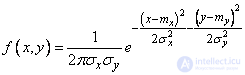9.1. Normal law on the plane . (9.1.9)

It is easy to make sure that random variables 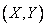9.1. Normal law on the plane , subject to the law of distribution with density (9.1.9), are not only uncorrelated, but also independent. Really.

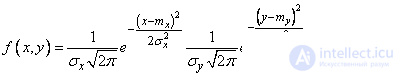9.1. Normal law on the plane .

those. the distribution density of the system is equal to the product of the distribution densities of the individual quantities in the system, which means that random variables 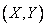9.1. Normal law on the plane are independent.

Thus, for a system of random variables subject to the normal law, their independence also follows from the uncorrelated values. The terms "uncorrelated" and "independent" values ​​for the case of normal distribution are equivalent.

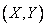With 9.1. Normal law on the plane random variables 9.1. Normal law on the plane are dependent. It is easy to verify, by calculating the conditional laws of distribution using formulas (8.4.6), that

9.1. Normal law on the plane

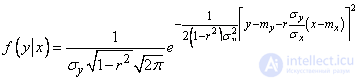Let's analyze one of these conditional distribution laws, for example 9.1. Normal law on the plane . To do this, convert the density expression 9.1. Normal law on the plane to the form:

9.1. Normal law on the plane .

Obviously, this is the density of a normal law with a center of dispersion

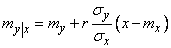9.1. Normal law on the plane (9.1.10)

and standard deviation

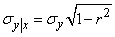9.1. Normal law on the plane . (9.1.11)

Formulas (9.1.10) and (9.1.11) show that in the conditional distribution law 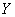9.1. Normal law on the plane with a fixed value 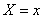9.1. Normal law on the plane only the expectation depends on this value, but not the variance.

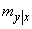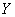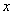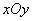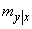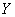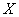Magnitude 9.1. Normal law on the plane called conditional expectation of magnitude 9.1. Normal law on the plane at this 9.1. Normal law on the plane . Dependence (9.1.10) can be represented on the plane 9.1. Normal law on the plane , deferring conditional expectation 9.1. Normal law on the plane y-axis. You’ll get a straight line called a regression line. 9.1. Normal law on the plane on 9.1. Normal law on the plane . Similarly straight

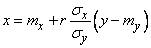9.1. Normal law on the plane (9.1.12)

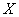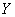there is a regression line 9.1. Normal law on the plane on 9.1. Normal law on the plane .

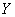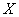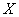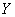Regression lines coincide only if there is a linear functional dependence 9.1. Normal law on the plane from 9.1. Normal law on the plane . With independent 9.1. Normal law on the plane and 9.1. Normal law on the plane regression lines are parallel to the coordinate axes.

Considering the expression (9.1.1) for the density of the normal distribution on the plane, we see that the normal law on the plane is completely determined by setting five parameters: the two coordinates of the center of dispersion 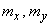9.1. Normal law on the plane two standard deviations 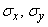9.1. Normal law on the plane and one correlation coefficient 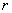9.1. Normal law on the plane . 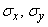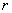In turn, the last three parameters 9.1. Normal law on the plane and 9.1. Normal law on the plane completely determined by the elements of the correlation matrix: dispersions 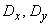9.1. Normal law on the plane and the correlation point 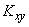9.1. Normal law on the plane . Thus, the minimum number of numerical characteristics of a system — mathematical expectations, variances, and the correlation moment — in the case when the system of subordination to the normal law determines the distribution law completely, i.e. forms a comprehensive system of characteristics.

Since in practice the normal law is quite common, it is often enough to set the minimum number — only five — of the numerical characteristics to fully characterize the distribution law of a system.

Comments

To leave a comment
If you have any suggestion, idea, thanks or comment, feel free to write. We really value feedback and are glad to hear your opinion.
To reply

Probability theory. Mathematical Statistics and Stochastic Analysis

Terms: Probability theory. Mathematical Statistics and Stochastic Analysis