Lecture
Probability density is one of the ways of defining a probability measure on a Euclidean space. 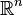 . In the case when the probability measure is the distribution of a random variable, we speak about the density of the random variable .
. In the case when the probability measure is the distribution of a random variable, we speak about the density of the random variable .
Let be 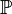 is a probability measure on
is a probability measure on 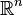 , that is, probabilistic space is defined
, that is, probabilistic space is defined 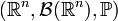 where
where 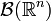 denotes the Borel σ-algebra on
denotes the Borel σ-algebra on 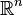 . Let be
. Let be 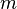 denotes the Lebesgue measure on
denotes the Lebesgue measure on 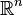 .
.
Definition 1. Probability 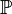 called absolutely continuous (relative to Lebesgue measure) (
called absolutely continuous (relative to Lebesgue measure) ( 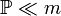 ), if any Borel set of zero Lebesgue measure also has a zero probability:
), if any Borel set of zero Lebesgue measure also has a zero probability:
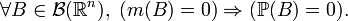
If the probability 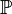 is absolutely continuous, then, according to the Radon – Nikodym theorem, there exists a nonnegative Borel function
is absolutely continuous, then, according to the Radon – Nikodym theorem, there exists a nonnegative Borel function 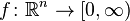 such that
such that
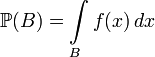 ,
, where common abbreviation is used 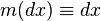 and the integral is understood in the sense of Lebesgue.
and the integral is understood in the sense of Lebesgue.
Definition 2. More generally, let 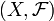 Is an arbitrary measurable space, and
Is an arbitrary measurable space, and 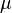 and
and 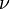 - two measures in this space. If there is a non-negative
- two measures in this space. If there is a non-negative 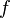 allowing to express measure
allowing to express measure 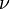 through measure
through measure 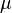 as
as
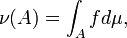
then this function is called the measure density 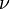 as
as 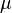 , or a derivative of Radon-Nikodym measures
, or a derivative of Radon-Nikodym measures 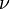 regarding measure
regarding measure 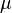 , and denote
, and denote
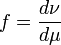 .
. 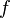 is probability density
is probability density 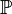 and
and 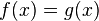 almost everywhere with respect to Lebesgue measure, then the function
almost everywhere with respect to Lebesgue measure, then the function 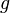 also is the probability density
also is the probability density 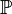 .
. 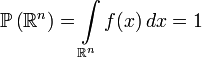 .
. Back if 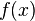 - non-negative i.e. function such that
- non-negative i.e. function such that 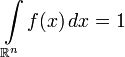 then there is an absolutely continuous probability measure
then there is an absolutely continuous probability measure 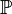 on
on 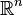 such that
such that 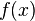 is its density.
is its density.
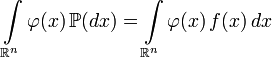 ,
, Where 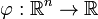 any Borel function that is integrable with respect to a probability measure
any Borel function that is integrable with respect to a probability measure 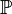 .
.
Let an arbitrary probability space be defined.  and
and 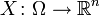 random variable (or random vector).
random variable (or random vector). 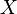 induces a probability measure
induces a probability measure 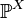 on
on 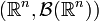 called the random distribution
called the random distribution 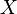 .
.
Definition 3. If the distribution 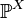 absolutely continuous with respect to Lebesgue measure, then its density
absolutely continuous with respect to Lebesgue measure, then its density 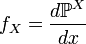 called random density
called random density 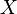 . The random variable itself
. The random variable itself 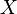 called absolutely continuous.
called absolutely continuous.
Thus for an absolutely continuous random variable we have:
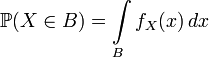 .
. 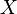 continuous and can be expressed in terms of density as follows:
continuous and can be expressed in terms of density as follows: 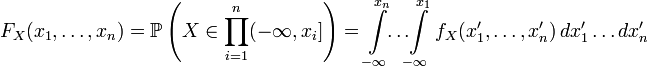 .
. In the one-dimensional case:
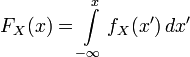 .
. If a 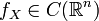 then
then 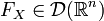 and
and
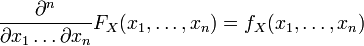 .
. In the one-dimensional case:
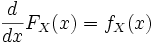 .
. 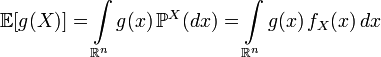 ,
, Where 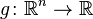 - Borel function, so
- Borel function, so 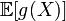 defined and of course.
defined and of course.
Let be 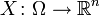 - an absolutely continuous random variable, and
- an absolutely continuous random variable, and 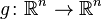 - injective continuously differentiable function such that
- injective continuously differentiable function such that 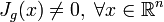 where
where 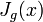 - Jacobian functions
- Jacobian functions 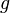 at the point
at the point 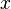 . Then a random variable
. Then a random variable 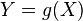 also absolutely continuous, and its density is:
also absolutely continuous, and its density is:
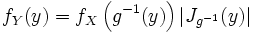 .
. In the one-dimensional case:
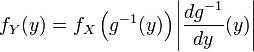 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis