Lecture
In the practical application of probability theory, one often encounters problems in which the same experience or similar experiments are repeated several times. As a result of each experience, some event may or may not appear. 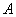 , and we are not interested in the result of each individual experience, but in the total number of occurrences
, and we are not interested in the result of each individual experience, but in the total number of occurrences 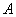 as a result of a series of experiments. For example, if a group of shots is made for the same goal, we are usually not interested in the result of each shot, but in the total number of hits. In such tasks, it is required to be able to determine the probability of any given number of occurrences of an event as a result of a series of experiments. Such tasks will be considered in this chapter. They are solved very simply in the case when the experiments are independent.
as a result of a series of experiments. For example, if a group of shots is made for the same goal, we are usually not interested in the result of each shot, but in the total number of hits. In such tasks, it is required to be able to determine the probability of any given number of occurrences of an event as a result of a series of experiments. Such tasks will be considered in this chapter. They are solved very simply in the case when the experiments are independent.
Several experiments are called independent if the probability of a particular outcome of each of the experiments does not depend on what outcomes other experiments had. For example, several consecutive coin toss are independent experiments. Several consecutive draws of a card from the deck are independent experiments, provided that the removed card is returned to the deck each time and the cards are shuffled; otherwise it is dependent experiences. Several shots are independent experiments only if the aiming is performed anew before each shot; in the case when the aiming is performed once before the whole shooting or is continuously carried out in the process of shooting (shooting by a queue, bombing by a series), the shots are dependent experiments. Independent experiments can be performed under the same or different conditions. In the first case, the probability of an event 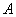 from experience to experience changes. The private theorem relates to the first case, and the general theorem on the repetition of experiments to the second. We will start with a particular theorem, as more elementary. First of all, consider a specific example.
from experience to experience changes. The private theorem relates to the first case, and the general theorem on the repetition of experiments to the second. We will start with a particular theorem, as more elementary. First of all, consider a specific example.
Example. Three independent shots are taken at the target, the probability of hitting it with each shot is equal to 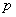 . Find the probability that with these three shots we get exactly two hits.
. Find the probability that with these three shots we get exactly two hits.
Decision. Denote 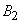 the event is that exactly two shells hit the target. This event can occur in three ways:
the event is that exactly two shells hit the target. This event can occur in three ways:
1) a hit on the first shot, a hit on the second, a miss on the third;
2) hit on the first shot, miss on the second, hit on the third;
3) a miss at the first shot, a hit on the second, a hit on the third.
Therefore, the event 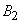 can be represented as the sum of the works of events:
can be represented as the sum of the works of events:
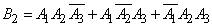 ,
,
Where 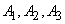 - hits at the first, second, third shots respectively,
- hits at the first, second, third shots respectively, 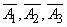 - a miss at the first, second, third shots.
- a miss at the first, second, third shots.
Considering that the three listed event options 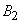 incompatible, and the events included in the works are independent, according to the theorems of addition and multiplication we get:
incompatible, and the events included in the works are independent, according to the theorems of addition and multiplication we get:
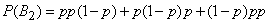 ,
,
or denoting 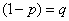 ,
,
 .
.
Similarly, by listing all possible options in which an event of interest to us may appear a given number of times, the following general task can be solved.
Produced by 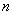 independent experiments, in each of which some event may or may not appear
independent experiments, in each of which some event may or may not appear 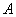 ; probability of occurrence
; probability of occurrence 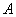 in each experience is equal
in each experience is equal 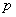 and the probability of non-occurrence
and the probability of non-occurrence 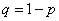 . Required to find the probability
. Required to find the probability 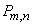 that event
that event 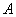 in these
in these 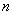 experiences will appear exactly
experiences will appear exactly 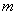 time.
time.
Consider an event 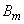 that event
that event 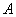 will appear in
will appear in 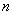 experiences exactly
experiences exactly 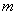 time. This event can be implemented in various ways. Decompose event
time. This event can be implemented in various ways. Decompose event 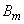 for the sum of the products of events consisting in the occurrence or non-occurrence
for the sum of the products of events consisting in the occurrence or non-occurrence 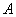 in a separate experience. We will denote
in a separate experience. We will denote 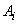 occurrence of an event
occurrence of an event 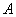 in the i-th experience;
in the i-th experience; 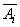 - non-event
- non-event 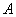 in the i-th experience.
in the i-th experience.
Obviously, each version of the event 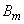 (each member of the sum) must consist of m occurrences
(each member of the sum) must consist of m occurrences 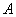 and
and 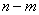 non-appearances, i.e. of
non-appearances, i.e. of 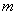 events
events 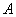 and
and 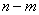 events
events 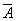 with different indices. In this way,
with different indices. In this way,
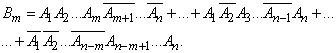
and in each work event 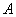 must enter
must enter 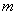 time as well
time as well 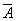 must enter
must enter 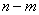 time.
time.
The number of all combinations of this kind is equal to 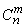 i.e. the number of ways that you can from
i.e. the number of ways that you can from 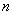 experiences choose
experiences choose 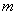 in which the event occurred
in which the event occurred 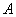 . The probability of each such combination, according to the multiplication theorem for independent events, is equal to
. The probability of each such combination, according to the multiplication theorem for independent events, is equal to 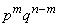 . Since combinations are incompatible with each other, then, by the addition theorem, the probability of an event
. Since combinations are incompatible with each other, then, by the addition theorem, the probability of an event 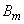 equals
equals
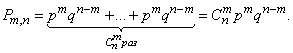
Thus, we can give the following formulation of a particular theorem on the repetition of experiments.
If produced 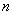 independent experiences in each of which the event
independent experiences in each of which the event 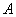 appears with probability
appears with probability 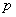 then the probability that an event
then the probability that an event 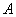 will appear exactly
will appear exactly 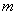 times expressed by the formula
times expressed by the formula
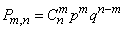 , (4.1.1)
, (4.1.1)
Where 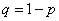 .
.
Formula (4.1.1) describes how probabilities are distributed between possible values of a certain random variable — the number of occurrences of the event. 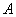 at
at 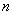 experiences.
experiences.
Due to the fact that the probabilities 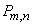 according to their form they are members of the binomial decomposition
according to their form they are members of the binomial decomposition 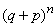 The probability distribution of the form (4.1.1) is called the binomial distribution.
The probability distribution of the form (4.1.1) is called the binomial distribution.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis