Lecture
In Chapter 7, we have already considered some of the problems of mathematical statistics related to the processing of experimental data. These were mainly the problem of finding the laws of the distribution of random greatness according to the results of experiments. To find the distribution law, you need to have sufficiently extensive statistical material, of the order of several hundred experiments (observations). However, in practice it is often necessary to deal with statistical material of a very limited scope — with two to three dozen observations, often even less. This is usually associated with the high cost and complexity of staging each experience. Such limited material is clearly not enough to find a previously unknown law of distribution of a random variable; but still this material can be processed and used to obtain some information about the random value. For example, on the basis of limited statistical material, it is possible to determine - at least tentatively - the most important numerical characteristics of a random variable: expectation, variance, and sometimes higher moments. In practice, it often happens that the form of the distribution law is known in advance, and it is required to find only some parameters on which it depends. For example, if it is known in advance that the distribution law of a random variable is normal, the processing task is reduced to determining its two parameters 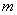 and
and  . If it is known in advance that the quantity is distributed according to the Poisson law, then only one of its parameters is to be determined: expectation
. If it is known in advance that the quantity is distributed according to the Poisson law, then only one of its parameters is to be determined: expectation 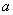 . Finally, in some problems, the form of the distribution law is generally insignificant, and only its numerical characteristics are required.
. Finally, in some problems, the form of the distribution law is generally insignificant, and only its numerical characteristics are required.
In this chapter, we will consider a number of problems on the determination of unknown parameters, on which the law of distribution of a random variable depends, but to a limited number of experiments.
First of all, it should be noted that any value of the desired parameter, calculated on the basis of a limited number of experiments, will always contain an element of randomness. Such an approximate, random value will be called a parameter estimate. For example, the arithmetic average of the observed values of a random variable in 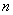 independent experiences. With a very large number of experiments, the arithmetic mean will most likely be very close to the expectation. If the number of experiments
independent experiences. With a very large number of experiments, the arithmetic mean will most likely be very close to the expectation. If the number of experiments 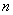 is small, then replacing the expectation with the arithmetic mean leads to some kind of error. This error is on average the greater the smaller the number of experiments. The same will be the case with estimates of other unknown parameters. Any of these estimates is random; when using it inevitable mistakes. It is advisable to choose such an assessment so that these errors are as minimal as possible.
is small, then replacing the expectation with the arithmetic mean leads to some kind of error. This error is on average the greater the smaller the number of experiments. The same will be the case with estimates of other unknown parameters. Any of these estimates is random; when using it inevitable mistakes. It is advisable to choose such an assessment so that these errors are as minimal as possible.
Consider the following general problem. There is a random variable 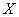 whose distribution law contains an unknown parameter
whose distribution law contains an unknown parameter 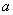 . It is required to find a suitable estimate for the parameter.
. It is required to find a suitable estimate for the parameter. 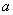 according to the results
according to the results 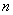 independent experiments, in each of which the magnitude
independent experiments, in each of which the magnitude 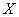 took a certain meaning.
took a certain meaning.
Denote the observed values of the random variable.
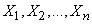 . (14.1.1)
. (14.1.1)
They can be considered as 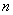 "Instances" of a random variable
"Instances" of a random variable 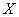 , i.e
, i.e 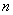 independent random variables, each of which is distributed according to the same law as the random variable
independent random variables, each of which is distributed according to the same law as the random variable 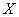 .
.
Denote 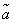 estimate for the parameter
estimate for the parameter 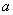 . Any estimate calculated from the material (14.1.1) must be a function of
. Any estimate calculated from the material (14.1.1) must be a function of 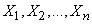 :
:
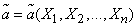 (14.1.2)
(14.1.2)
and, therefore, is itself random. Distribution law 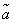 depends, firstly, on the distribution law
depends, firstly, on the distribution law 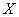 (and, in particular, from the most unknown parameter
(and, in particular, from the most unknown parameter 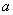 ); secondly, on the number of experiments
); secondly, on the number of experiments 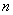 . In principle, this distribution law can be found by known methods of probability theory.
. In principle, this distribution law can be found by known methods of probability theory.
Present to the assessment 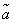 a series of requirements that it must satisfy in order to be in some sense a “benign” assessment.
a series of requirements that it must satisfy in order to be in some sense a “benign” assessment.
Naturally require evaluation 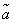 so that with an increase in the number of experiences
so that with an increase in the number of experiences 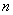 it approached (converged in probability) to the parameter
it approached (converged in probability) to the parameter 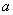 . An assessment possessing such a property is called consistent.
. An assessment possessing such a property is called consistent.
In addition, it is desirable that, using the value 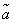 instead
instead 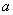 , we at least did not make a systematic error in the direction of overestimation or understatement, i.e., that the condition
, we at least did not make a systematic error in the direction of overestimation or understatement, i.e., that the condition
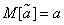 . (14.1.3)
. (14.1.3)
An estimate satisfying this condition is called unbiased.
Finally, it is desirable that the selected unbiased estimate has the smallest variance compared with others, i.e.
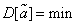 . (14.1.4)
. (14.1.4)
An estimate possessing such a property is called effective.
In practice, it is not always possible to satisfy all these requirements. For example, it may turn out that, even if an effective estimate exists, the formulas for calculating it turn out to be too complicated, and one has to be satisfied with another estimate, the variance of which is somewhat larger. Sometimes, in the interests of ease of calculation, slightly biased estimates are used. However, the choice of evaluation should always be preceded by its critical consideration from all the points of view listed above.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis