Lecture
In presenting the theory of transformation of random functions, we will use the concept of an operator widely used in mathematics and technology.
The concept of an operator is a generalization of the concept of a function. When we establish a functional connection between two variables 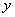 and
and 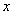 and write:
and write:
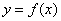 . (15.6.1)
. (15.6.1)
then under the symbol 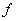 we understand the rule by which the given value
we understand the rule by which the given value 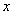 quite definite value is matched
quite definite value is matched 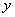 . Sign
. Sign 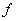 there is a symbol of some transformation to which it is necessary to subject the value
there is a symbol of some transformation to which it is necessary to subject the value 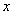 , To obtain
, To obtain 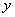 . Accordingly, the type of this transformation functions can be linear and nonlinear, algebraic, transcendental, etc.
. Accordingly, the type of this transformation functions can be linear and nonlinear, algebraic, transcendental, etc.
Similar concepts and the corresponding symbols are applied in mathematics and in those cases when not values, but functions are subjected to conversion.
Consider some function 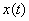 and set a certain rule
and set a certain rule 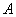 according to which function
according to which function 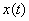 converted to another function
converted to another function 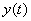 . We write this transformation in the following form:
. We write this transformation in the following form:
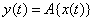 . (15.6.2)
. (15.6.2)
Examples of such transformations can be, for example, differentiation:
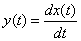 , (15.6.3)
, (15.6.3)
integration:
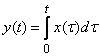 , (15.6.4)
, (15.6.4)
etc.
Rule 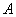 according to which function
according to which function 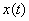 converted to function
converted to function 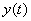 , we will call the operator; for example, we will say: the differentiation operator, the integration operator, the operator of the solution of a differential equation, etc.
, we will call the operator; for example, we will say: the differentiation operator, the integration operator, the operator of the solution of a differential equation, etc.
Defining the operator, we considered only the transformation function 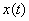 to another function
to another function 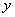 same argument
same argument 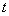 . It should be noted that such a preservation of the argument when defining the operator is not at all mandatory: the operator can convert the function
. It should be noted that such a preservation of the argument when defining the operator is not at all mandatory: the operator can convert the function 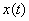 to a function of another argument
to a function of another argument 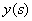 , eg:
, eg:
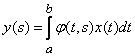 , (15.6.5)
, (15.6.5)
Where 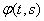 - some function dependent, besides argument
- some function dependent, besides argument 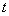 , also from parameter
, also from parameter 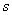 .
.
But since when analyzing errors of dynamic systems, the most natural argument is time 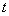 , we will limit ourselves here to considering operators that transform a single argument function.
, we will limit ourselves here to considering operators that transform a single argument function. 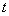 to another function of the same argument.
to another function of the same argument.
If a dynamic system converts a function arriving at its input 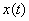 in function
in function 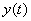 :
:
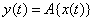 ,
,
that operator 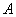 is called a dynamic system operator.
is called a dynamic system operator.
In the more general case, not one but several functions arrive at the system input; equally, several functions may appear at the output of the system; in this case, the system operator converts one set of functions into another. However, for the sake of simplicity, we consider here only the most elementary case of the transformation of one function into another.
Transformations or operators applied to functions can be of various types. The most important for practice is the class of so-called linear operators.
Operator 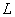 is called linear homogeneous if it has the following properties:
is called linear homogeneous if it has the following properties:
1) the operator can be applied by term to the sum of functions:
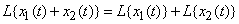 ; (15.6.6)
; (15.6.6)
2) constant value 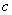 can be taken out of the operator sign:
can be taken out of the operator sign:
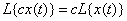 . (15.6.7)
. (15.6.7)
From the second property, by the way, it follows that for a linear homogeneous operator the property
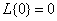 , (15.6.8)
, (15.6.8)
that is, at zero input, the response of the system is zero.
Examples of linear homogeneous operators:
1) differentiation operator:
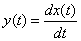 ;
;
2) integration operator:
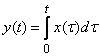 ;
;
3) the operator of multiplication by a certain function 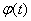 :
:
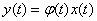 ,
,
4) integration operator with a given "weight" 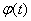 :
:
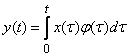
etc.
In addition to linear homogeneous operators, there are also linear inhomogeneous operators.
Operator 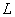 is called linear inhomogeneous if it consists of a linear homogeneous operator with the addition of some well-defined function
is called linear inhomogeneous if it consists of a linear homogeneous operator with the addition of some well-defined function 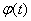 :
:
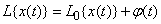 , (15.6.9)
, (15.6.9)
Where 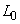 - linear homogeneous operator.
- linear homogeneous operator.
Examples of linear inhomogeneous operators:
one) 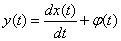 ,
,
2)  ,
,
3) 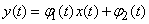 .
.
Where 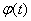 ,
, 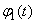 ,
, 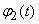 - well-defined functions, and
- well-defined functions, and 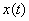 - function convertible by operator.
- function convertible by operator.
In mathematics and engineering, the conventional form of recording operators, similar to algebraic symbolism, is widely used. Such symbolism in some cases allows to avoid complex transformations and write formulas in a simple and convenient form.
For example, the operator of differentiation is often denoted by the letter 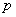 :
:
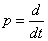 ,
,
placed as a multiplier in front of the expression to be differentiated. With this record
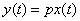
tantamount to writing
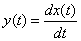 .
.
Double differentiation is indicated by a multiplier. 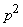 :
:
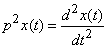
etc.
Using such symbolism, in particular, it is very convenient to write down differential equations.
Let, for example, the work of a dynamic system 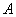 described by a linear differential equation with constant coefficients relating the response of the system
described by a linear differential equation with constant coefficients relating the response of the system 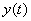 with impact
with impact 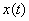 . In the usual notation, this differential equation has the form:
. In the usual notation, this differential equation has the form:
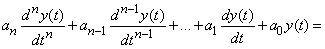
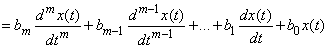 . (15.6.10)
. (15.6.10)
In symbolic form, this equation can be written as:
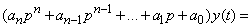
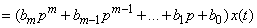 .
.
Where 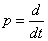 - differentiation operator.
- differentiation operator.
Denoting for short polynomials with respect to 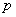 in right and left parts
in right and left parts
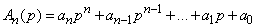 ,
,
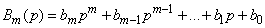 ,
,
we write the equation in an even more compact form:
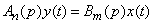 . (15.6.11)
. (15.6.11)
Finally, formally solving equation (15.6.11) with respect to 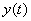 , you can symbolically write the solution operator of a linear differential equation in “explicit” form:
, you can symbolically write the solution operator of a linear differential equation in “explicit” form:
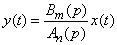 . (15.6.12)
. (15.6.12)
Using the same symbolism, one can also write in the operator form a linear differential equation with variable coefficients. In its usual form, this equation has the form:
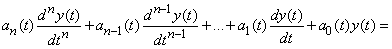
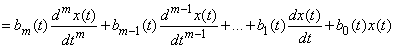 . (15.6.13)
. (15.6.13)
Denoting polynomials relatively 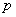 whose coefficients depend on
whose coefficients depend on
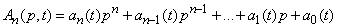 ,
,
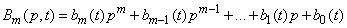 ,
,
You can write a differential equation operator in the form:
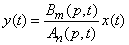 . (15.6.14)
. (15.6.14)
In the future, as necessary, we will use such a symbolic form of recording operators.
The dynamic systems encountered in engineering are often described by linear differential equations. In this case, as is easily seen, the system operator is linear.
A dynamic system whose operator is linear is called a linear dynamic system.
In contrast to linear operators and systems, non-linear systems and operators are considered. Examples of nonlinear operators can serve
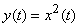 ,
, 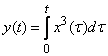 ,
, 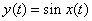 ,
,
as well as solving a nonlinear differential equation, at least
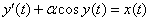 .
.
A dynamic system whose operator is not linear is called a nonlinear system.
In practice, linear systems are very common. In connection with the linearity of these systems, the apparatus of the theory of random functions can be applied with great efficiency to the analysis of their errors. Just as the numerical characteristics of linear functions of ordinary random variables can be obtained from the numerical characteristics of the arguments, the characteristics of a random function at the output of a linear dynamic system can be determined if the operator of the system and the characteristics of a random function at its input are known.
Even more often than linear systems, in practice there are systems that are not strictly linear, but within certain limits that allow linearization. If random perturbations at the system input are small enough, then almost any system can be considered - within these small perturbations - as approximately linear, just as with sufficiently small random changes of the arguments, almost any function can be linearized.
Approximation of approximate linearization of differential equations is widely used in the theory of errors of dynamic systems.
In the future, we will consider only linear (or linearizable) dynamical systems and the corresponding linear operators.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis