Lecture
In practice, it is often necessary to consider systems of more than two random variables. These systems are interpreted as random points or random vectors in the space of a certain number of dimensions.
We give examples.
1. The point of rupture of a remote projectile in space is characterized by three Cartesian coordinates 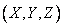 or three spherical coordinates
or three spherical coordinates 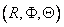 .
.
2. The whole 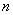 consecutive measurements of varying magnitude
consecutive measurements of varying magnitude 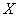 - system
- system 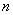 random variables
random variables 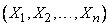 .
.
3. Shoots a burst from 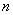 shells. Set of coordinates
shells. Set of coordinates 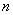 points of contact on the plane - system
points of contact on the plane - system  random variables (abscissa and ordinate points of hitting):
random variables (abscissa and ordinate points of hitting):
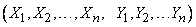 .
.
4. The initial velocity of the fragment is a random vector, characterized by three random variables: the magnitude of the velocity 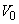 and two corners
and two corners 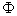 and
and 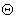 defining the direction of flight of the fragment in a spherical coordinate system.
defining the direction of flight of the fragment in a spherical coordinate system.
A complete characteristic of a system of an arbitrary number of random variables is the distribution law of the system, which can be given by a distribution function or a distribution density.
System distribution function 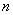 random variables
random variables 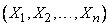 called the probability of sharing
called the probability of sharing 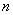 inequalities of the form
inequalities of the form 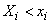 :
:
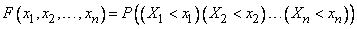 . (8.7.1)
. (8.7.1)
Distribution density system 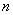 continuous random variables called
continuous random variables called 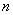 -th mixed partial derivative of a function
-th mixed partial derivative of a function 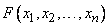 taken once for each argument:
taken once for each argument:
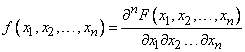 . (8.7.2)
. (8.7.2)
Knowing the law of distribution of the system, it is possible to determine the laws of distribution of individual quantities included in the system. The distribution function of each of the quantities included in the system is obtained if the distribution function sets all other arguments equal 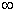 :
:
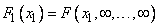 . (8.7.3)
. (8.7.3)
If you select from the system of values 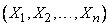 private system
private system 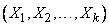 , the distribution function of this system is determined by the formula
, the distribution function of this system is determined by the formula
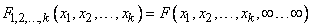 . (8.7.4)
. (8.7.4)
The density of distribution of each of the quantities in the system is obtained if the density of the distribution of the system is integrated in infinite limits over all other arguments:
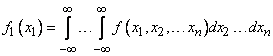 . (8.7.5)
. (8.7.5)
The distribution density of the private system 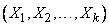 allocated from the system
allocated from the system 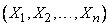 , is equal to:
, is equal to:
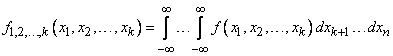 (8.7.0)
(8.7.0)
Conditional law of the distribution of the private system 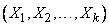 its distribution law, calculated under the condition that the other quantities
its distribution law, calculated under the condition that the other quantities 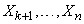 took meaning
took meaning 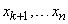 .
.
The conditional distribution density can be calculated by the formula
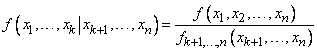 (8.7.7)
(8.7.7)
Random variables 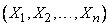 are called independent if the distribution law of each private system separated from the system
are called independent if the distribution law of each private system separated from the system 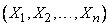 , does not depend on what values the remaining random variables took.
, does not depend on what values the remaining random variables took.
The distribution density of a system of independent random variables is equal to the product of the distribution densities of the individual variables in the system:
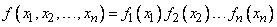 (8.7.8)
(8.7.8)
Probability of hitting a random point 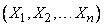 within
within 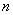 -dimensional area
-dimensional area 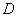 is expressed
is expressed 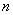 -fold integral:
-fold integral:
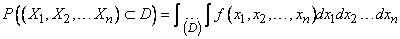 . (8.7.9)
. (8.7.9)
Formula (8.7.9) is essentially the basic formula for calculating the probabilities of events that are not reducible to the case diagram. Indeed, if the event we are interested in 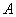 does not boil down to the scheme of cases, its probability cannot be calculated directly. If it is not possible to make a sufficient number of homogeneous experiments and approximately determine the probability of an event
does not boil down to the scheme of cases, its probability cannot be calculated directly. If it is not possible to make a sufficient number of homogeneous experiments and approximately determine the probability of an event 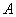 in terms of its frequency, the typical scheme for calculating the probability of an event is as follows. Transition from the scheme of events to the scheme of random variables (most often - continuous) and reduce the event
in terms of its frequency, the typical scheme for calculating the probability of an event is as follows. Transition from the scheme of events to the scheme of random variables (most often - continuous) and reduce the event 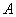 to the event that the system of random variables
to the event that the system of random variables 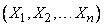 will be within a certain area
will be within a certain area 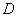 . Then the probability of an event
. Then the probability of an event 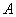 can be calculated by the formula (8.7.9).
can be calculated by the formula (8.7.9).
Example 1. An airplane is hit by a remote projectile, provided that the projectile rupture occurred not further than at a distance. 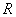 from the aircraft (more precisely, from the conditional point on the axis of the aircraft, taken as its center). The law of distribution of the points of rupture of a remote projectile in the coordinate system associated with the target has a density
from the aircraft (more precisely, from the conditional point on the axis of the aircraft, taken as its center). The law of distribution of the points of rupture of a remote projectile in the coordinate system associated with the target has a density 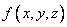 . Determine the probability of hitting the aircraft.
. Determine the probability of hitting the aircraft.
Decision. Denoting the defeat of the aircraft by the letter 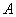 , we have:
, we have:
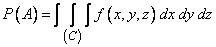 ,
,
where integration extends over the ball 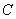 radius
radius 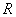 centered at the origin.
centered at the origin.
Example 2. A meteorite encountered on the path of an artificial Earth satellite breaks through its envelope if: 1) the angle 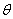 under which a meteorite meets the surface of a satellite is enclosed within certain limits.
under which a meteorite meets the surface of a satellite is enclosed within certain limits. 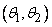 ; 2) the meteorite has a weight of at least
; 2) the meteorite has a weight of at least 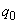 (d) and 3) the relative speed of a meteorite meeting a satellite is less
(d) and 3) the relative speed of a meteorite meeting a satellite is less 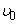 (m / s). Meeting speed
(m / s). Meeting speed 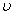 meteorite weight
meteorite weight 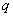 and the angle of the meeting
and the angle of the meeting 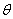 represent a system of random variables with a distribution density
represent a system of random variables with a distribution density 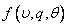 . Find probability
. Find probability 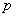 the fact that a separate meteorite hit the satellite, breaks through its shell.
the fact that a separate meteorite hit the satellite, breaks through its shell.
Decision. Integrating distribution density 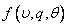 on the three-dimensional region corresponding to the punching of the shell, we get:
on the three-dimensional region corresponding to the punching of the shell, we get:
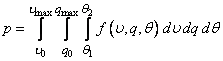 ,
,
Where 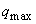 - maximum meteorite weight,
- maximum meteorite weight,  - Maximum meeting speed.
- Maximum meeting speed.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis