11.4. Refinement of the results obtained by the method of linearization

In some problems of practice, there is doubt about the applicability of the linearization method due to the fact that the range of changes of random arguments is not so small that within it the function can be linearized with sufficient accuracy.

In these cases, to verify the applicability of the linearization method and to refine the results obtained, a method can be applied based on preserving in the decomposition of a function not only linear members, but also some subsequent higher-order terms and an estimate of the errors associated with these members.

In order to clarify this method, we first consider the simplest case of a function of one random argument. Random value 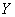there is a function of random argument :

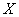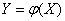, (11.4.1)

and function relatively little different from the linear on the branch of practically possible values ​​of the argument 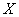, but still differs so much that there is doubt about the applicability of the linearization method. To check this circumstance, we apply a more accurate method, namely: decompose the function in taylor series in a neighborhood of a point 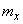and keep in decomposition the first three members:

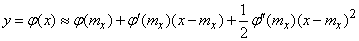. (11.4.2)

The same formula will obviously approximate random variables. 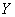and :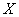

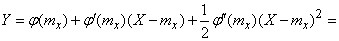
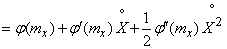. (11.4.3)

Using the expression (11.4.3), we find the expectation and variance of 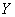. Applying the theorems on numerical characteristics, we have:

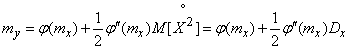. (11.4.4)

According to the formula (11.4.4) you can find the adjusted value of the expectation and compare it with the value 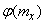which is obtained by the linearization method; the amendment taking into account the nonlinearity of the function is the second term of formula (11.4.4).

Determining the variance of the right and left side of the formula (11.4.3), we have:

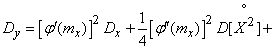
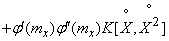, (11.4.5)

Where 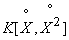- correlation moment of magnitudes .

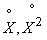We express the quantities entering the formula (11.4.5) through the central moments of the quantities :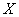

,

.

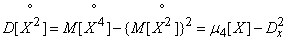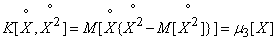Finally we have:

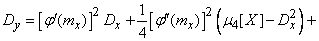
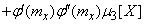. (11.4.6)

Formula (11.4.6) gives a refined value of the variance compared to the linearization method; its second and third terms represent the correction for the nonlinearity of the function. In the formula, except for the variance of the argument 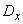, includes the third and fourth central points 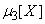, . If these moments are known, then the correction to the variance can be found directly by the formula (11.4.6). However, it is often not necessary to define it precisely; it is enough to know its order. In practice, there are often random variables distributed approximately according to the normal law. For a random variable subject to normal law,

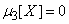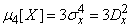, , (11.4.7)

and the formula (11.4.6) takes the form:

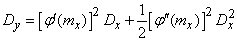. (11.4.8)

Formula (11.4.8) can be used for an approximate estimate of the error of the linearization method in the case when the argument is distributed according to a law close to normal.

A completely similar method can be applied to the function of several random arguments:

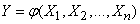. (11.4.9)

Decomposing function

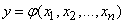
in taylor series in a neighborhood of a point 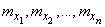and keeping in the expansion terms not higher than second order, we have approximately:

,

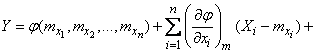
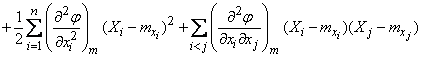or by entering centered values,

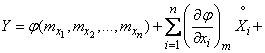
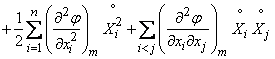, (11.4.10)

where is the index 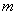still denotes that in a partial derivative expression instead of arguments 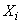their mathematical expectations are substituted .

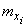Applying to the formula (11.4.10) the operation of mathematical expectation, we have:

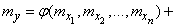
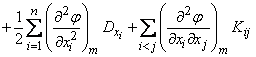, (11.4.11)

Where 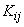- correlation moment of magnitudes .

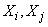In the most important case for practice, when the arguments 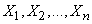uncorrelated, the formula (11.4.11) takes the form:

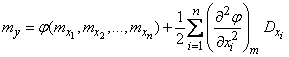. (11.4.12)

The second term of formula (11.4.12) is the correction for the nonlinearity of the function.

Let us proceed to the determination of the variance of 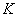. To get the expression of dispersion in the simplest form, suppose that the quantities 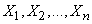not only uncorrelated, but also independent. Determining the variance of the right and left side (11.4.10) and using the theorem on the dispersion of a product (see 10.2), we get:

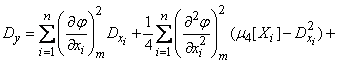
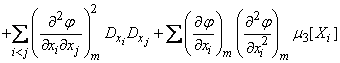. (11.4.13)

For quantities distributed according to a law close to normal, you can use the formula (11.4.7) and convert the expression (11.4.13) to the form:

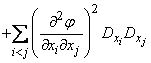. (11.4.14)

The last two terms in expression (11.4.14) are the “correction for non-linearity of the function” and can serve to estimate the accuracy of the linearization method when calculating the variance.