Lecture
In practical applications of probability theory, very often one encounters problems in which the result of an experiment is described not by one random variable, but by two or more random variables that form a complex or system. For example, the point of impact of the projectile is determined not by one random variable, but by two: the abscissa and the ordinate - and can be considered as a complex of two random greatness. Similarly, the point of rupture of a remote projectile is determined by a set of three random variables. When shooting a group of 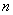 shots a set of points of impact on the plane can be considered as a complex or system
shots a set of points of impact on the plane can be considered as a complex or system 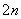 random variables:
random variables: 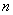 abscissa and
abscissa and 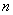 ordinate points of impact. The splinter formed when the projectile is broken is characterized by a number of random variables: weight, size, initial speed, direction of flight, etc. We agree on a system of several random variables
ordinate points of impact. The splinter formed when the projectile is broken is characterized by a number of random variables: weight, size, initial speed, direction of flight, etc. We agree on a system of several random variables 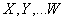 denote
denote 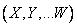 .
.
The properties of a system of several random variables are not exhausted by the properties of the individual variables that make it up: in addition, they also include interrelations (dependencies) between random variables.
When considering issues related to systems of random variables, it is convenient to use the geometric interpretation of the system. For example, a system of two random variables 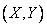 can be represented as a random point on a plane with coordinates
can be represented as a random point on a plane with coordinates 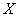 and
and 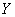 (Fig. 8.1.1). Similarly, a system of three random variables can be depicted as a random point in three-dimensional space. It is often convenient to talk about the system.
(Fig. 8.1.1). Similarly, a system of three random variables can be depicted as a random point in three-dimensional space. It is often convenient to talk about the system. 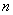 random variables as a "random point in space
random variables as a "random point in space 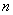 measurements. Despite the fact that the latter interpretation does not have direct visibility, its use gives some gain in terms of common terminology and simplification of the records.
measurements. Despite the fact that the latter interpretation does not have direct visibility, its use gives some gain in terms of common terminology and simplification of the records.
Often, instead of the image of a random point, the image of a random vector is used for the geometric interpretation of a system of random variables. A system of two random variables is considered as a random vector on the plane. 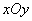 whose components along the axes are random variables
whose components along the axes are random variables 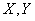 (Fig. 8.1.2). The system of three random variables is represented by a random vector in three-dimensional space, the system
(Fig. 8.1.2). The system of three random variables is represented by a random vector in three-dimensional space, the system 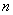 random variables - random vector in space
random variables - random vector in space 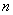 measurements. In this case, the theory of random number systems is considered as a theory of random vectors.
measurements. In this case, the theory of random number systems is considered as a theory of random vectors.
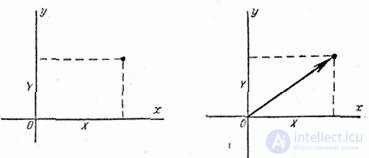
Fig.8.1.1. Fig.8.1.2
In this course, we will, depending on the convenience of the overlay, use both one and the other interpretation.
Being engaged in systems of random variables, we will consider both complete, exhaustive probabilistic characteristics — laws of distribution, and incomplete — numerical characteristics.
We begin the presentation with the simplest case of a system of two random variables.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis