Lecture
In the previous 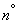 we got acquainted with the method of directly determining the characteristics of a random function from experience. This method is not always used. First, the formulation of special experiments designed to study random functions of interest to us can be very complicated and expensive. Secondly, we often need to investigate random functions that characterize the errors of instruments, sighting devices, control systems, etc., that are not yet existing, but only designed or developed. At the same time, the study of these errors is usually undertaken precisely in order to rationally select the design parameters of the system so that they lead to minimal errors. It is clear that in this case a direct study of random functions that characterize the operation of the system is inexpedient, and in some cases it is impossible at all. In such cases, not direct, but indirect methods of investigating random functions are used as the main working methods. We have already used similar indirect methods in the study of random variables: a series of chapters in our course - ch. 10, 11, 12 - was devoted to finding the laws of distribution and the numerical characteristics of random variables indirectly, according to the laws of distribution and the numerical characteristics of other random greatness associated with them. Using completely analogous methods, one can determine the characteristics of random functions indirectly, by the characteristics of other random functions associated with them. The development of such indirect methods is the main content of the applied theory of random functions.
we got acquainted with the method of directly determining the characteristics of a random function from experience. This method is not always used. First, the formulation of special experiments designed to study random functions of interest to us can be very complicated and expensive. Secondly, we often need to investigate random functions that characterize the errors of instruments, sighting devices, control systems, etc., that are not yet existing, but only designed or developed. At the same time, the study of these errors is usually undertaken precisely in order to rationally select the design parameters of the system so that they lead to minimal errors. It is clear that in this case a direct study of random functions that characterize the operation of the system is inexpedient, and in some cases it is impossible at all. In such cases, not direct, but indirect methods of investigating random functions are used as the main working methods. We have already used similar indirect methods in the study of random variables: a series of chapters in our course - ch. 10, 11, 12 - was devoted to finding the laws of distribution and the numerical characteristics of random variables indirectly, according to the laws of distribution and the numerical characteristics of other random greatness associated with them. Using completely analogous methods, one can determine the characteristics of random functions indirectly, by the characteristics of other random functions associated with them. The development of such indirect methods is the main content of the applied theory of random functions.
The task of indirectly studying random functions in practice usually arises in the following form.
There is some dynamic system 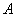 ; By "dynamic system" we mean any device, sight, computer-solving mechanism, automatic control system, etc. This system can be mechanical, electrical, or contain any other elements. We will imagine the work of the system as follows: some input data is continuously being received at the input of the system; the system processes them and continuously produces some result. We agree to call the data arriving at the system input: “impact”, and the output result is the “reaction” of the system to this effect. The effects may include varying voltages, angular and linear coordinates of any objects, signals or commands given to the control system, etc. In the same way, the response of the system can be generated in one form or another: in the form of voltages, angular displacements etc. For example, for an airborne sight, the impact is the angular coordinate of a moving target, which is continuously measured during the tracking process, the reaction is the preemptive angle.
; By "dynamic system" we mean any device, sight, computer-solving mechanism, automatic control system, etc. This system can be mechanical, electrical, or contain any other elements. We will imagine the work of the system as follows: some input data is continuously being received at the input of the system; the system processes them and continuously produces some result. We agree to call the data arriving at the system input: “impact”, and the output result is the “reaction” of the system to this effect. The effects may include varying voltages, angular and linear coordinates of any objects, signals or commands given to the control system, etc. In the same way, the response of the system can be generated in one form or another: in the form of voltages, angular displacements etc. For example, for an airborne sight, the impact is the angular coordinate of a moving target, which is continuously measured during the tracking process, the reaction is the preemptive angle.
Consider the simplest case: when the system input 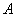 only one impact is served, which is a function of time
only one impact is served, which is a function of time 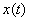 : system response to this effect is another function of time
: system response to this effect is another function of time 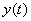 . System operation diagram
. System operation diagram 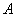 conventionally depicted in Fig. 15.5.1.
conventionally depicted in Fig. 15.5.1.

Fig. 15.5.1.
Let's say that the system 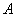 performs on the input action some transformation, as a result of which the function
performs on the input action some transformation, as a result of which the function 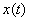 converted to another function
converted to another function 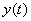 . We write this transformation symbolically in the form:
. We write this transformation symbolically in the form:
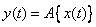 . (15.5.1)
. (15.5.1)
Transformation 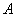 may be of any kind and of any complexity. In the simplest cases, for example, multiplication by a given multiplier (amplifiers, multiplying mechanisms), differentiation or integration (differentiating or integrating devices). However, in practice, systems that perform such simple transformations in their pure form are almost never encountered; As a rule, the operation of the system is described by differential equations, and the transformation
may be of any kind and of any complexity. In the simplest cases, for example, multiplication by a given multiplier (amplifiers, multiplying mechanisms), differentiation or integration (differentiating or integrating devices). However, in practice, systems that perform such simple transformations in their pure form are almost never encountered; As a rule, the operation of the system is described by differential equations, and the transformation 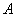 comes down to solving a differential equation linking effects
comes down to solving a differential equation linking effects 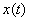 with reaction
with reaction 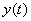 .
.
In the study of a dynamic system, the main task is solved first: for a given effect 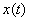 determine system response
determine system response 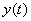 . However, for such a complete study of the system and evaluation of its technical qualities, such an elementary approach is insufficient. In effect
. However, for such a complete study of the system and evaluation of its technical qualities, such an elementary approach is insufficient. In effect 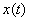 never arrives at the system input in its pure form: it is always distorted by some random errors (disturbances), as a result of which an unspecified function actually affects the system
never arrives at the system input in its pure form: it is always distorted by some random errors (disturbances), as a result of which an unspecified function actually affects the system 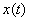 and random function
and random function 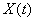 ; accordingly, the system produces a random function as a reaction.
; accordingly, the system produces a random function as a reaction. 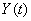 also different from the theoretical reaction
also different from the theoretical reaction 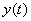 (fig. 15.5.2).
(fig. 15.5.2).
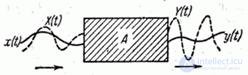
Fig. 15.5.2.
The question naturally arises: how large will the random distortions of the reaction of the system be in the presence of random disturbances at its input? And further: how should the system parameters be selected so that these distortions are minimal?
The solution of such problems cannot be obtained by the methods of classical probability theory; the only suitable mathematical apparatus for this purpose is the apparatus of the theory of random functions.
Of the two tasks set above, naturally, the simpler one is the first — the direct — task. We formulate it as follows.
To dynamic system input 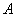 random function arrives
random function arrives 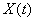 ; the system subjects it to a known transformation, with the result that a random function appears at the system output:
; the system subjects it to a known transformation, with the result that a random function appears at the system output:
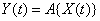 . (15.5.2)
. (15.5.2)
The characteristics of the random function are known. 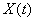 : expectation and correlation function. It is required to find similar characteristics of a random function.
: expectation and correlation function. It is required to find similar characteristics of a random function. 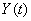 . In short: according to the given characteristics of a random function at the input of a dynamic system, find the characteristics of a random function at the output.
. In short: according to the given characteristics of a random function at the input of a dynamic system, find the characteristics of a random function at the output.
The task can be solved absolutely exactly in one particular, but very important for the practice case: when the transformation 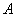 belongs to the class of so-called linear transformations and accordingly the system
belongs to the class of so-called linear transformations and accordingly the system 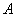 belongs to the class of linear systems.
belongs to the class of linear systems.
The contents of these concepts will be explained in the following.  .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis