Numerical Characteristics of Random Variables

Expected value. The mathematical expectation of a discrete random variable X that takes a finite number of values x i with probabilities p i is the sum:

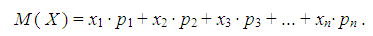(6 a )

The mathematical expectation of a continuous random variable X is the integral of the product of its x values and the probability distribution density f ( x ):

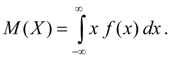(6 b )

The improper integral (6 b ) is assumed to be absolutely convergent (otherwise it is said that the mathematical expectation M ( X ) does not exist). Mathematical expectation characterizes the average value of the random variable X. Its dimension coincides with the dimension of a random variable.

Properties of expectation:

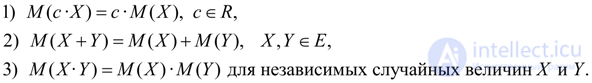(7)

Dispersion. The variance of the random variable X is the number:

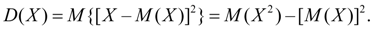(eight)

Dispersion is a characteristic of the dispersion of values ​​of a random variable X relative to its average value M ( X ). The dimension of the variance is equal to the dimension of the random variable squared. Based on the definitions of variance (8) and the mathematical expectation (5) for a discrete random variable and (6) for a continuous random variable, we obtain similar expressions for the variance:

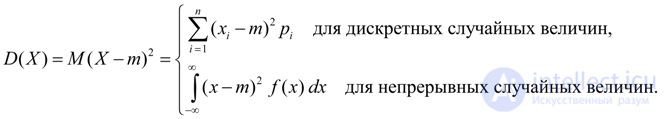(9)

Here m = M ( X ).

Dispersion properties:

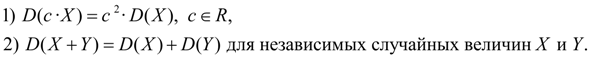(ten)

Standard deviation:

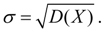(eleven)

Since the dimension of the standard deviation is the same as that of a random variable, it is more often than the variance used as a measure of scattering.

Moments of distribution. The concepts of mathematical expectation and variance are special cases of a more general concept for the numerical characteristics of random variables — moments of distribution . The moments of the distribution of a random variable are introduced as the mathematical expectations of some of the simplest functions of a random variable. So, the moment of order k relative to the point x 0 is the mathematical expectation M ( X - x 0 ) k . Moments relative to the origin x = 0 are called initial moments and are designated:

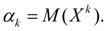(12)

The initial moment of the first order is the distribution center of the considered random variable:

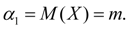(13)

Moments relative to the center of distribution x = m are called central moments and are denoted by:

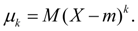(14)

From (7) it follows that the central moment of the first order is always zero:

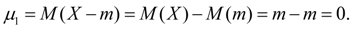(15)

The central moments do not depend on the origin of the values ​​of the random variable, because when shifted by a constant value C, its distribution center shifts by the same value C , and the deviation from the center does not change: X - m = ( X - C ) - ( m - C ).
Now it is obvious that the variance is the central moment of the second order :

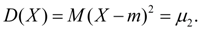(sixteen)

Asymmetry. The central moment of the third order:

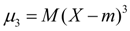(17)

serves to assess the asymmetry of the distribution . If the distribution is symmetrical about the point x = m , then the third moment of the third order will be equal to zero (like all the central moments of odd orders). Therefore, if the central moment of the third order is non-zero, then the distribution cannot be symmetric. The value of asymmetry is estimated using a dimensionless asymmetry coefficient :

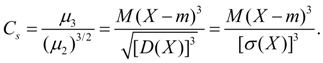(18)

The sign of the asymmetry coefficient (18) indicates a right-handed or left-handed asymmetry (Fig. 2).

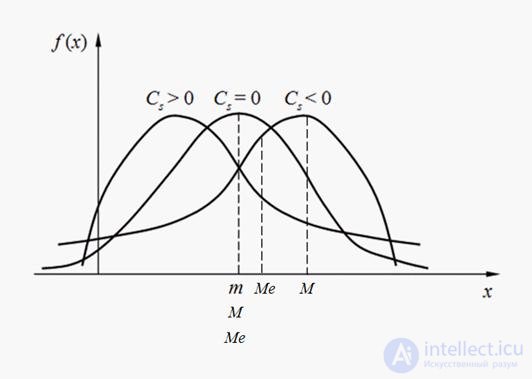
Fig. 2. Types of asymmetry of distributions.

Excess. The central moment of the fourth order:

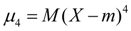(nineteen)

serves to evaluate the so-called kurtosis , which determines the degree of toughness (sharpness) of the distribution curve near the distribution center with respect to the normal distribution curve. Since for normal distribution 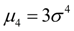, then the value is taken as an excess:

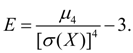(20)

In fig. 3 shows examples of distribution curves with different values ​​of kurtosis. For a normal distribution, Е = 0. Curves that are more pointed than normal, have positive kurtosis, and flat-tops are negative.

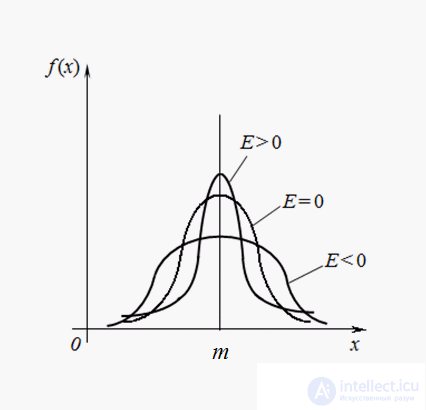
Fig. 3. Distribution curves with varying degrees of coolness (kurtosis).

Moments of higher orders in engineering applications of mathematical statistics usually do not apply.

A discrete random mode is its most likely value. The mode of a continuous random variable is called its value at which the probability density is maximum (Fig. 2). If the distribution curve has one maximum, then the distribution is called unimodal . If the distribution curve has more than one maximum, then the distribution is called polymodal . Sometimes there are distributions, the curves of which have not a maximum, but a minimum. Such distributions are called antimodal . In the general case, the mode and the expectation of a random variable do not coincide. In the particular case of modal , i.e. having a mode, symmetric distribution, and provided that there is a mathematical expectation, the latter coincides with the mode and center of symmetry of the distribution.

The median of the random variable X is its value Me , for which equality holds: 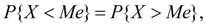those. it is equally likely that the random variable X will be less than or greater than Me . Geometrically, the median is the abscissa of the point at which the area under the distribution curve is divided in half (Fig. 2). In the case of a symmetric modal distribution, the median, mode and expectation coincide.