Lecture
Given a system of random variables 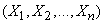 subordinate to the normal distribution law (or, in short, “formally distributed”); random value
subordinate to the normal distribution law (or, in short, “formally distributed”); random value 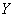 is a linear function of these quantities:
is a linear function of these quantities:
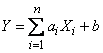 . (12.7.1)
. (12.7.1)
It is required to find the distribution law 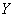 .
.
It is easy to verify that this is a normal law. Indeed, the magnitude 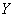 is the sum of linear functions, each of which depends on one normally distributed argument
is the sum of linear functions, each of which depends on one normally distributed argument 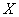 , and it was proved above that such a linear function is also normally distributed. Adding several normally distributed random variables, we again obtain the value normally distributed.
, and it was proved above that such a linear function is also normally distributed. Adding several normally distributed random variables, we again obtain the value normally distributed.
It remains to find the parameters of 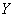 - center of dispersion
- center of dispersion 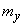 and standard deviation
and standard deviation 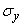 . Applying the theorems on the expectation and variance of a linear function, we obtain:
. Applying the theorems on the expectation and variance of a linear function, we obtain:
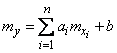 , (12.7.2)
, (12.7.2)
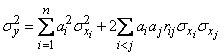 , (12.7.3)
, (12.7.3)
Where 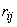 - coefficient of correlation of quantities
- coefficient of correlation of quantities 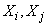 .
.
In the case where the values 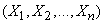 uncorrelated (and therefore, under normal law, and independent), the formula (12.7.3) takes the form:
uncorrelated (and therefore, under normal law, and independent), the formula (12.7.3) takes the form:
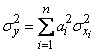 . (12.7.4)
. (12.7.4)
The standard deviations in formulas (12.7.3) and (12.7.4) can be replaced by proportional probable deviations.
In practice, it is often the case that the laws of the distribution of random variables 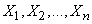 included in the formula (12.7.1) are not exactly known, only their numerical characteristics are known: mathematical expectations and variances. If at the same time values
included in the formula (12.7.1) are not exactly known, only their numerical characteristics are known: mathematical expectations and variances. If at the same time values 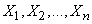 independent and their number
independent and their number 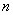 is large enough, so, as a rule, it can be argued that, regardless of the form of the laws of distribution of quantities
is large enough, so, as a rule, it can be argued that, regardless of the form of the laws of distribution of quantities 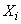 , distribution law
, distribution law 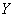 close to normal. In practice, to obtain a distribution law, which can be approximately taken as normal, it is usually sufficient
close to normal. In practice, to obtain a distribution law, which can be approximately taken as normal, it is usually sufficient 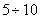 terms in expression (12.7.1). It should be noted that this does not apply to the case when the dispersion of one of the terms in the formula (12.7.1) is overwhelmingly large compared to all the others; it is assumed that random terms in the sum (12.7.1) in their scattering have approximately the same order. If these conditions are met, then for
terms in expression (12.7.1). It should be noted that this does not apply to the case when the dispersion of one of the terms in the formula (12.7.1) is overwhelmingly large compared to all the others; it is assumed that random terms in the sum (12.7.1) in their scattering have approximately the same order. If these conditions are met, then for 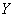 a normal law can be approximately adopted with the parameters defined by formulas (12.7.2) and (12.7.4).
a normal law can be approximately adopted with the parameters defined by formulas (12.7.2) and (12.7.4).
Obviously, all the above considerations about the distribution law of a linear function are valid (of course, the approximation is also for the case when the function is not exactly linear, but can be linearized).
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis