Lecture
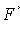
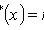
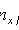
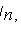
where n x is the number of sample values less than x ; n is the sample size.
(unbiased, consistent estimate of the expectation)
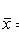
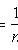
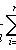
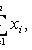
where x i - sample values; n is the sample size.
(biased, consistent estimate of variance)
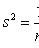
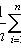
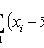
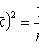
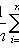
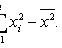
(unbiased, consistent estimate of variance)
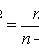
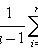
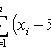
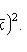
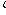
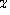distribution of random variable X In the discrete case
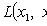
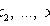
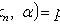
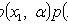
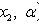
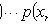
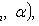
Where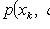 
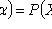
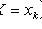
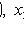
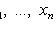- sample values.
In absolutely continuous case
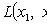
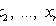
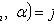
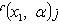
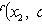
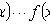
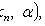
Where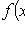 
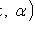- distribution density X.
1. For a mathematical expectation with a known variance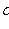 
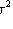
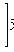
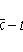
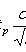
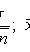
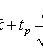
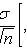
where t p is the root of the equation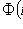 
; 
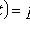
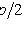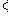
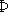- Laplace function.
2. For mathematical expectation with unknown variance
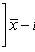
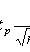
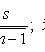
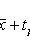
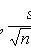
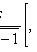
s 2 is the sample variance; t p satisfies the condition P (| t n-1 | < t p ) = p ; t n-1 is a random variable distributed according to Student’s law with n - 1 degrees of freedom.
3. For dispersion
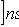
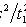
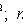
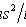
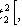
Where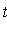 
, 
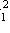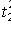
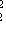are from the conditions:
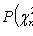
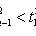
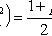
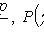
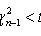
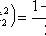
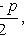
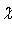
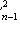- random variable distributed by law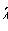 
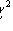with n - 1 degrees of freedom.
Selective correlation moment of X and Y values
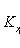
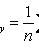
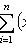
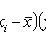
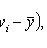
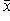
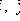
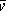- sample averages X and Y, respectively.
Selective correlation coefficient
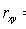
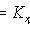
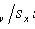
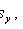
Where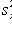 
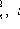
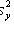- selective dispersions of X and Y values.
Selective regression coefficient Y to X
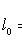
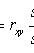
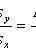
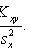
Selective regression equation
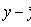
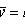
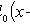
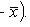
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis