12.3. The distribution law of a nonmonotonic function of one random argument

There is a continuous random variable 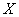with distribution density 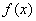; other value 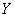associated with 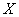functional dependence:

,

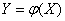and function 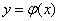Location on possible values ​​of the argument are not monotonous (Fig. 12.3.1).

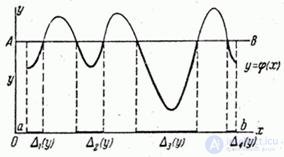
Fig. 12.3.1.

Find the distribution function 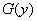magnitudes 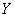. To do this, again, hold the line 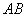parallel to the abscissa at a distance 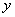from it and select those parts of the curve 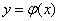on which the condition is met 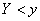. Let these sections correspond to the sections of the x-axis: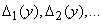

Event 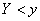tantamount to hitting a random variable 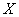on one of the sites 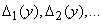- all the same on which one. therefore

.

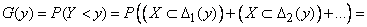
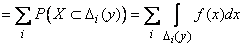Thus, for the distribution function of 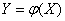we have the formula:

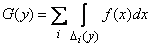. (12.3.1)

Spacing boundaries 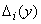depends on 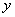and given the specific form of the function 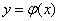can be expressed as explicit functions 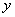. Differentiating 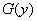by size 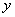entering the limits of integrals, we obtain the distribution density of :

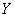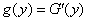. (12.3.2)

Example. Magnitude 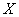subject to the law of uniform density in the area from 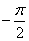before :

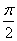Find the law of distribution of magnitude .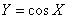

Decision. Build a graph of the function 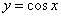(fig. 12.3.2). Obviously 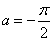, 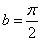and in the interval 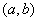function 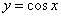not monotonous.

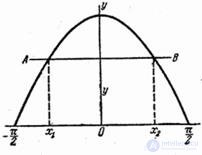
Fig. 12.3.2.

Applying the formula (12.3.1), we have:

.

Express limits 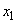and 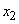through :

; .

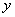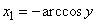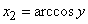From here

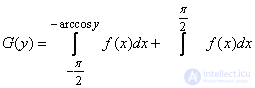. (12.3.3)

To find the density We will not calculate the integrals in the formula (12.3.3), but directly differentiate this expression with respect to the variable within the integrals:

.

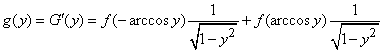Bearing in mind that 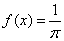, we get:

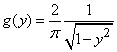. (12.3.4)

Pointing for 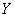distribution law (12.3.4), it should be stipulated that it is valid only in the range from 0 to 1, i.e. within the limits in which it changes 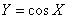with argument 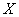between 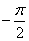and 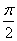. Beyond these limits the density 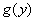equals zero.

Function graph 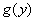given in fig. 12.3.3. With 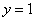curve 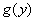has a branch going to infinity.

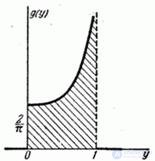
Fig. 12.3.3.